Prim(프림) 알고리즘
그래프의 모든 정점을 최소 비용으로 연결하는, 즉, 최소 신장 트리를 구현하는 대표적인 Greedy(탐욕) 알고리즘이다.
Greedy 알고리즘
- 그 순간에 가장 좋다고 생각되는 해를 선택
- MST에 포함된 정점들과 그렇지 않은 정점들을 잇는 간선중 가장 가중치가 작은 간선을 선택하여 MST에 추가
- 그 순간에는 최적의 해일 수 있지만, 전체적으로 봤을때는 그렇지 않을 수 있으므로 반드시 검증을 해야함
- 정점이 이미 선택되어 MST에 포함되어 있는지 검증
- Kruskal(크루스칼) 알고리즘의 경우는 간선을 선택하는 Greedy 알고리즘이다.
동작방식
- 임의의 정점을 출발 정점으로 선택
- 매 단계에서 이전단계에 MST에 포함된 정점들과 포함되지 않은 정점들을 잇는 간선 중 가중치가 가장 작은 간선을 선택하여 MST를 확장한다.
- 간선개수가
Visualize

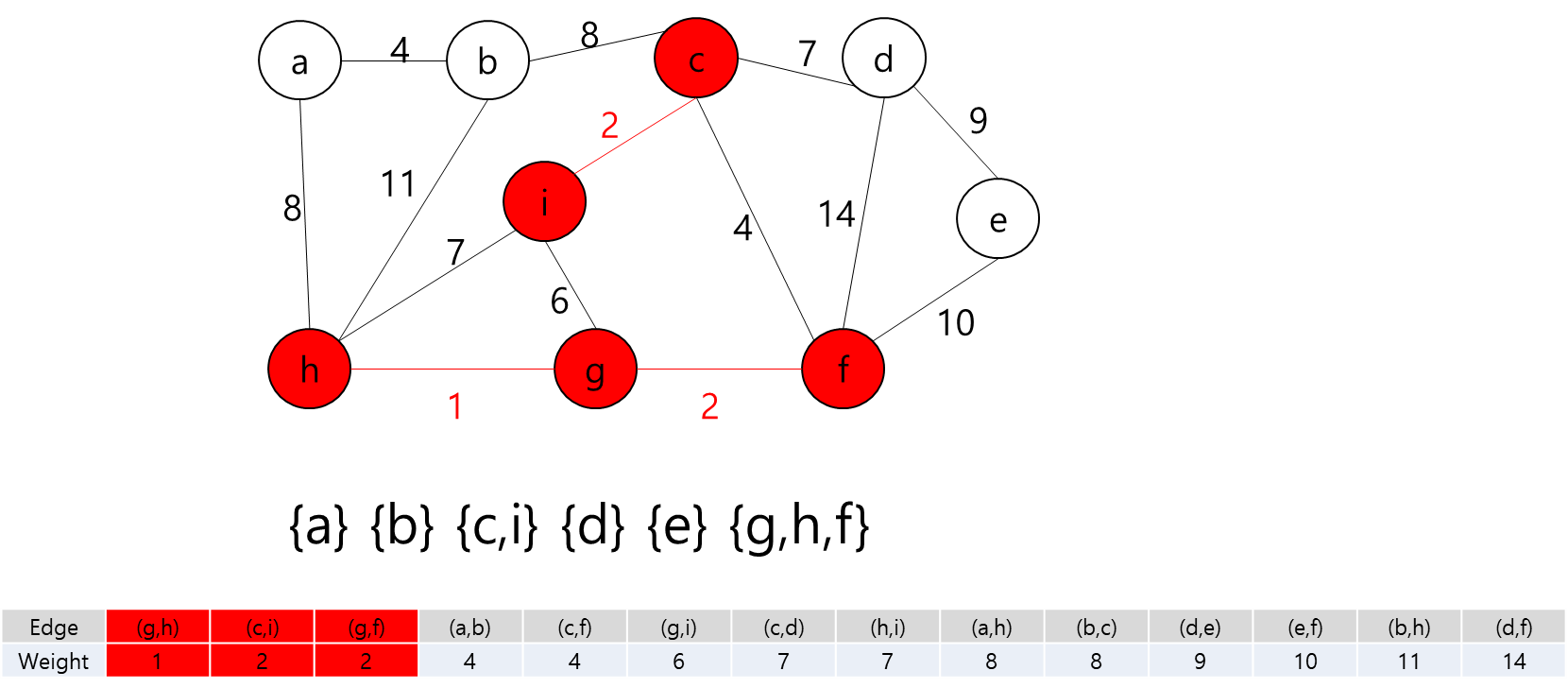
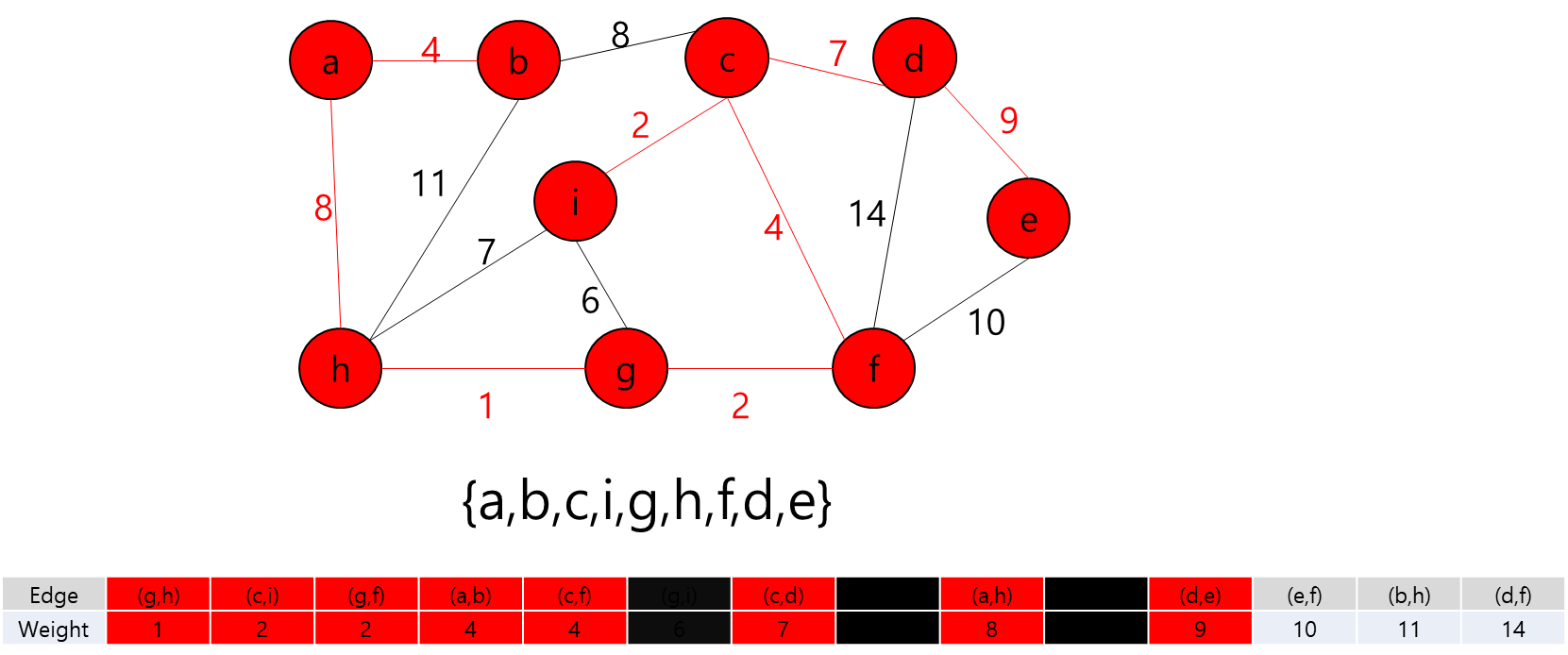
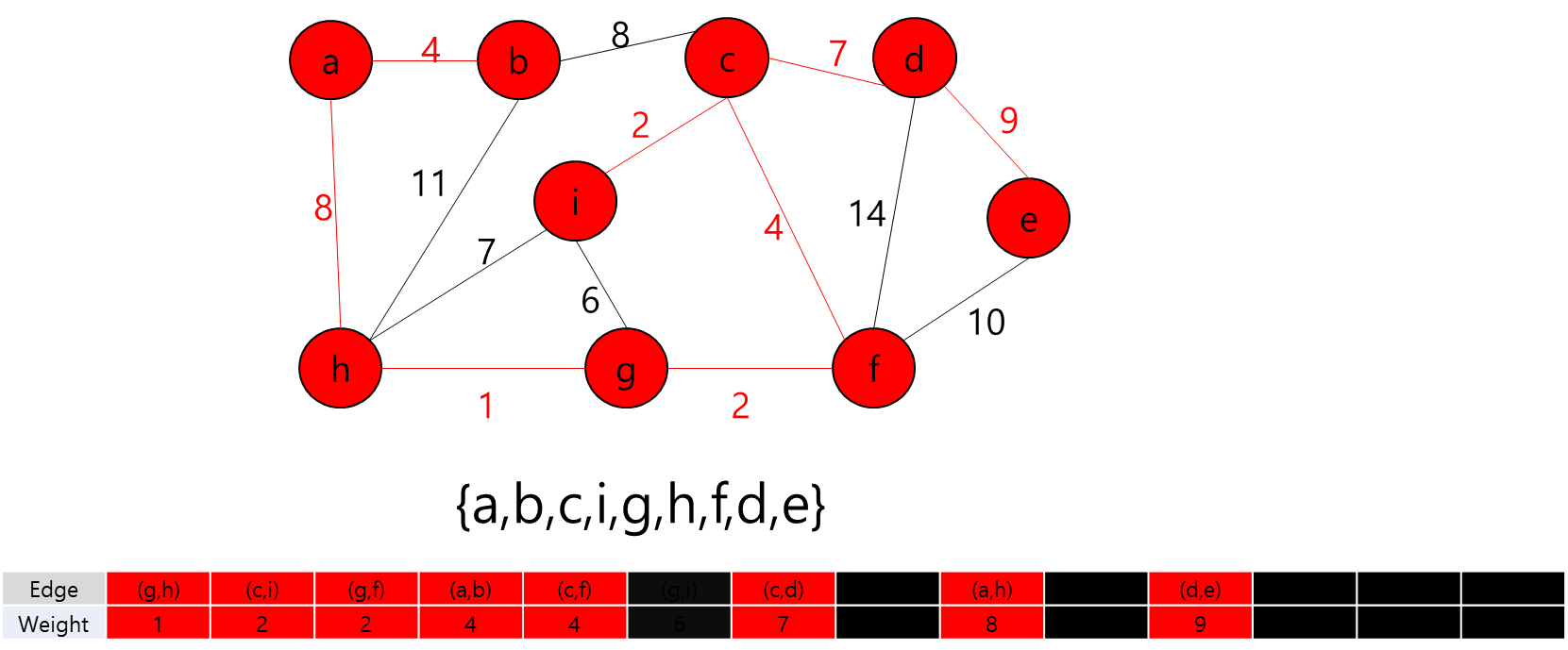
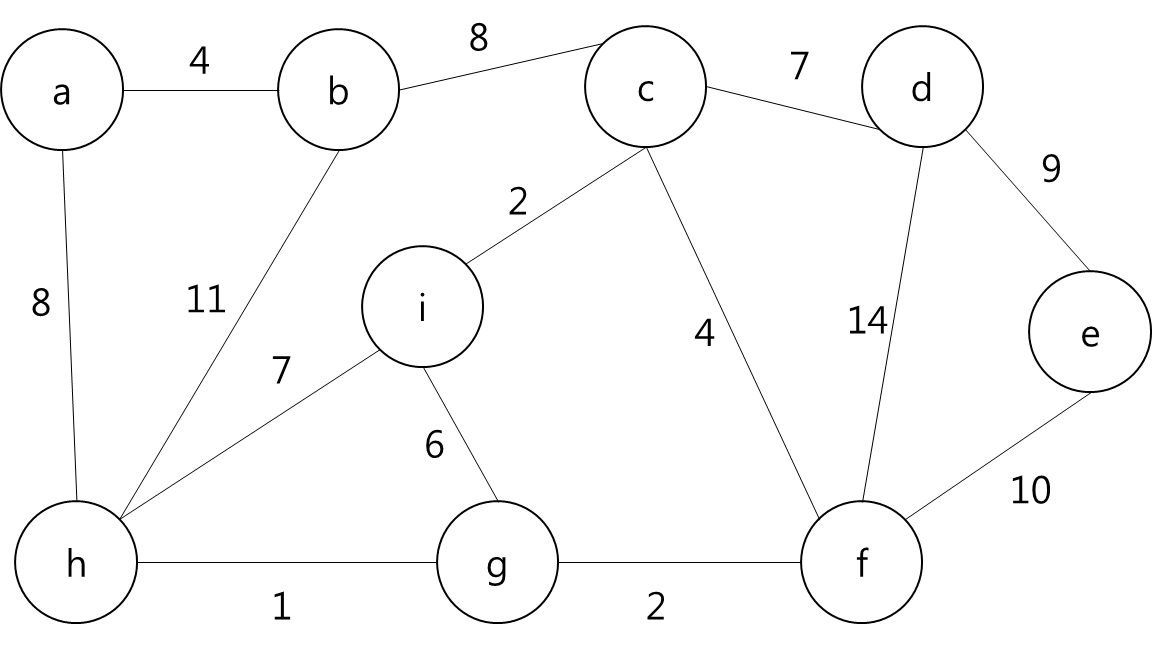
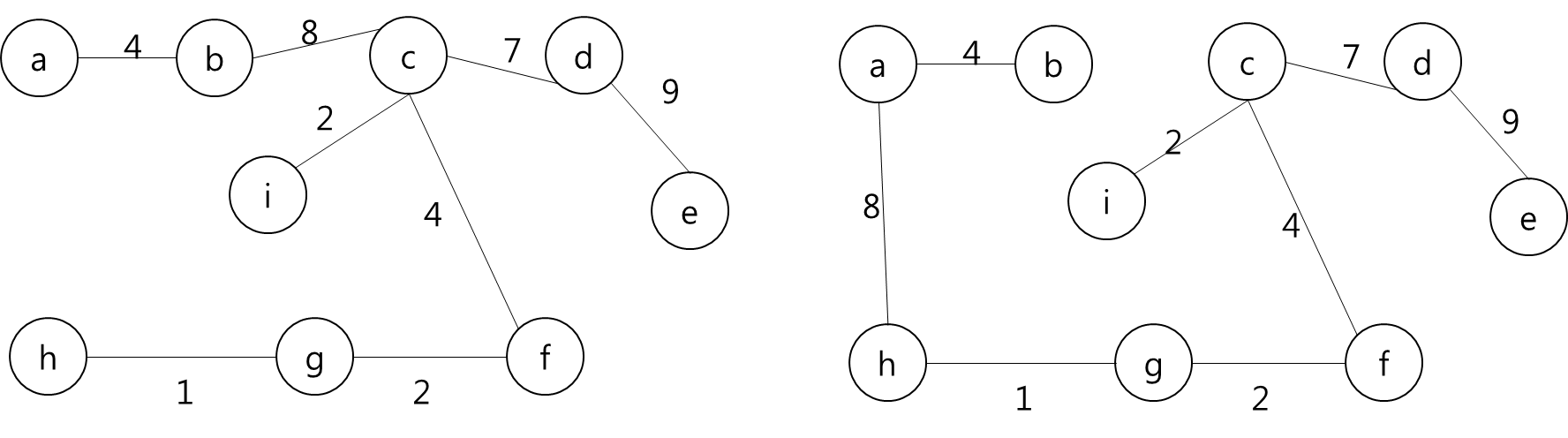
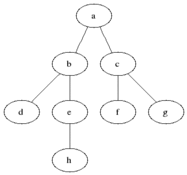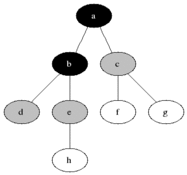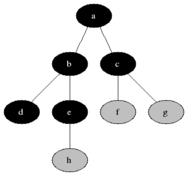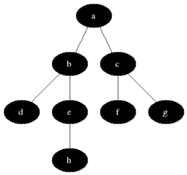
임의의 정점 a를 선택한다.

MST에 포함된 정점들(a)과 그렇지 않은 정점들을 잇는 간선들 중에 가중치가 가장 작은 간선 (a,b)를 MST에 추가

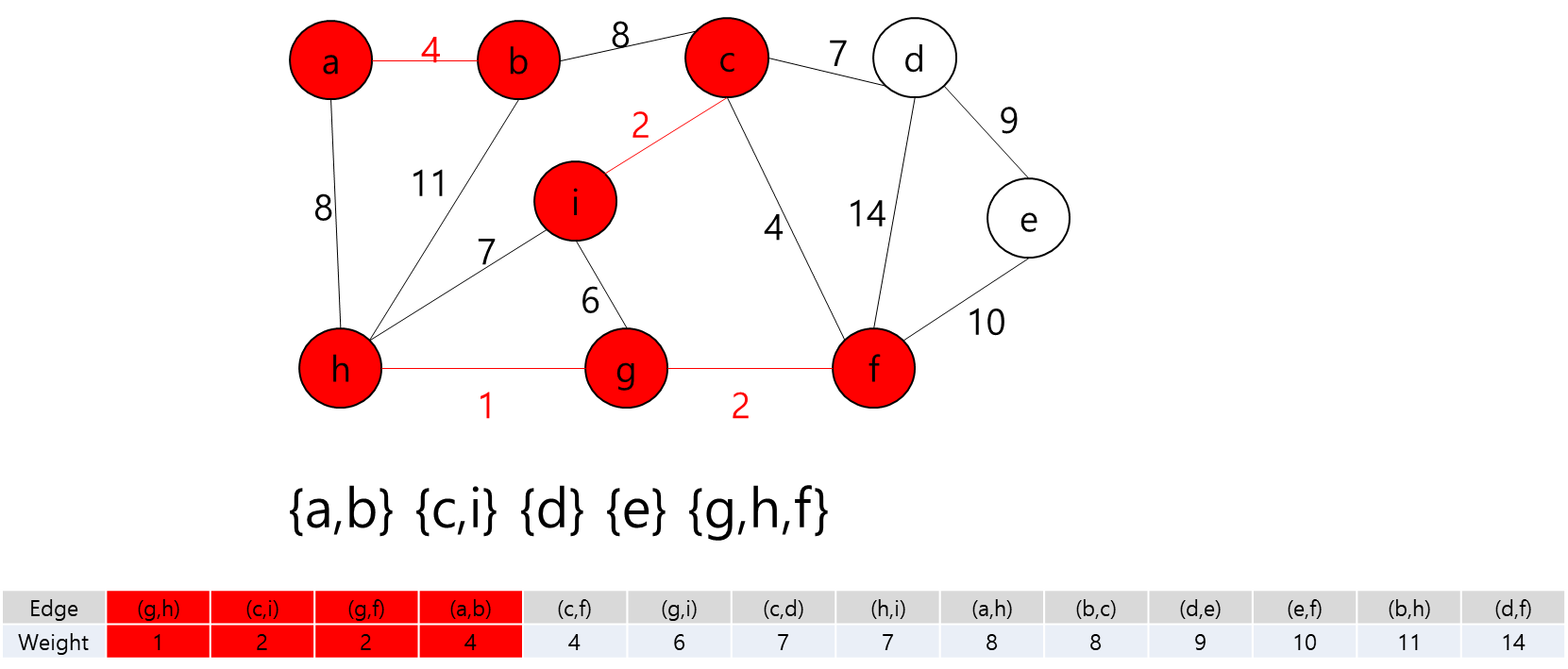
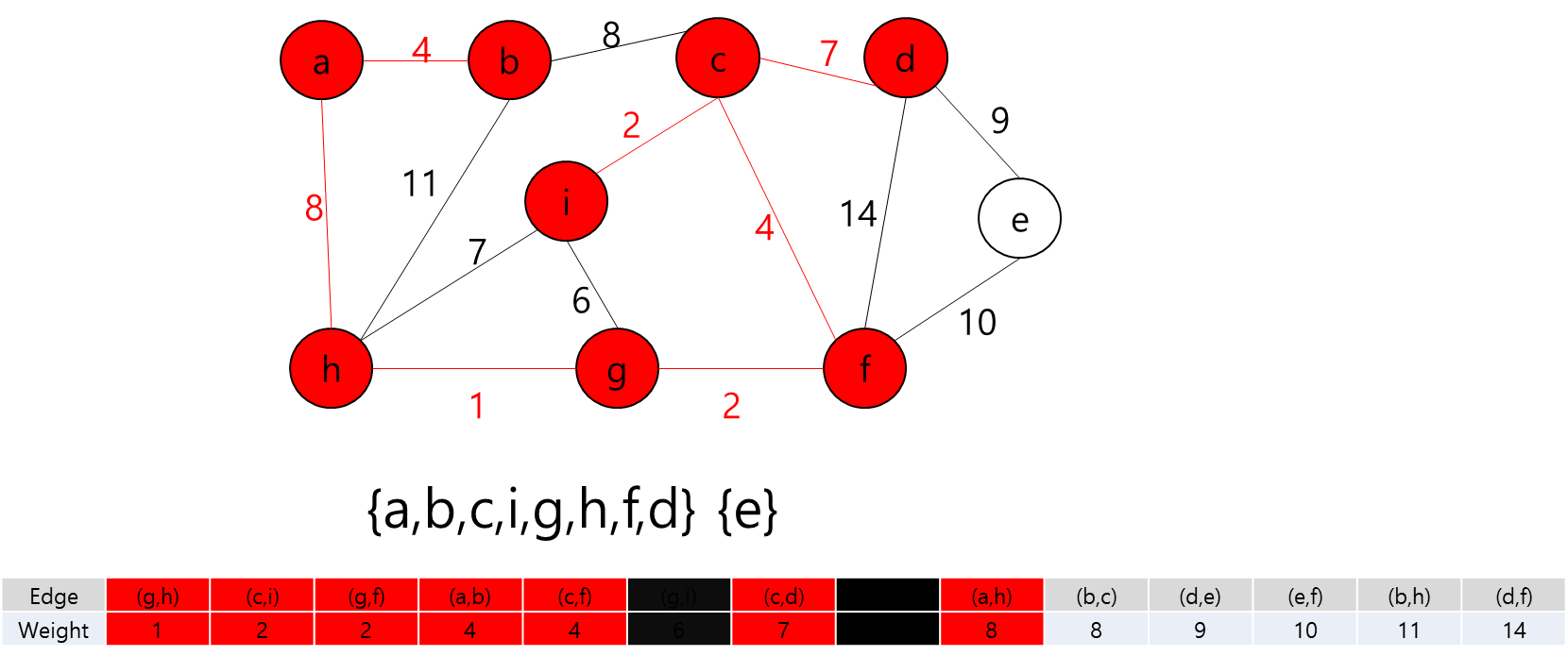
MST에 포함된 정점들(a,b)과 그렇지 않은 정점들을 잇는 간선 중 가중치가 가장 작은 간선((a,h))를 MST에 추가

MST에 포함된 정점들(a,b,h)과 그렇지 않은 정점들을 잇는 간선 중 가중치가 가장 작은 간선((h,g))를 MST에 추가
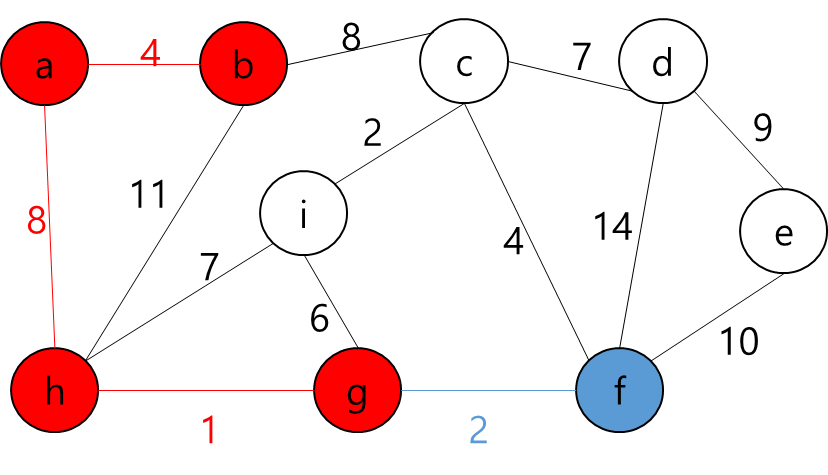
MST에 포함된 정점들(a,b,h,g)과 그렇지 않은 정점들을 잇는 간선 중 가중치가 가장 작은 간선((g,f))를 MST에 추가
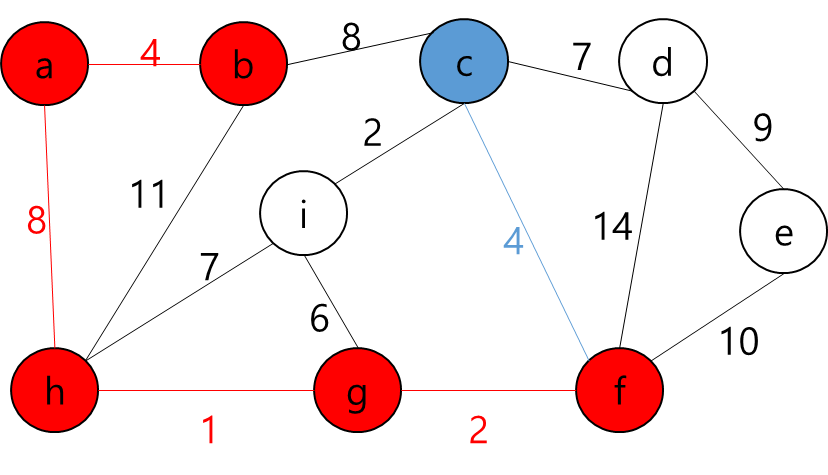
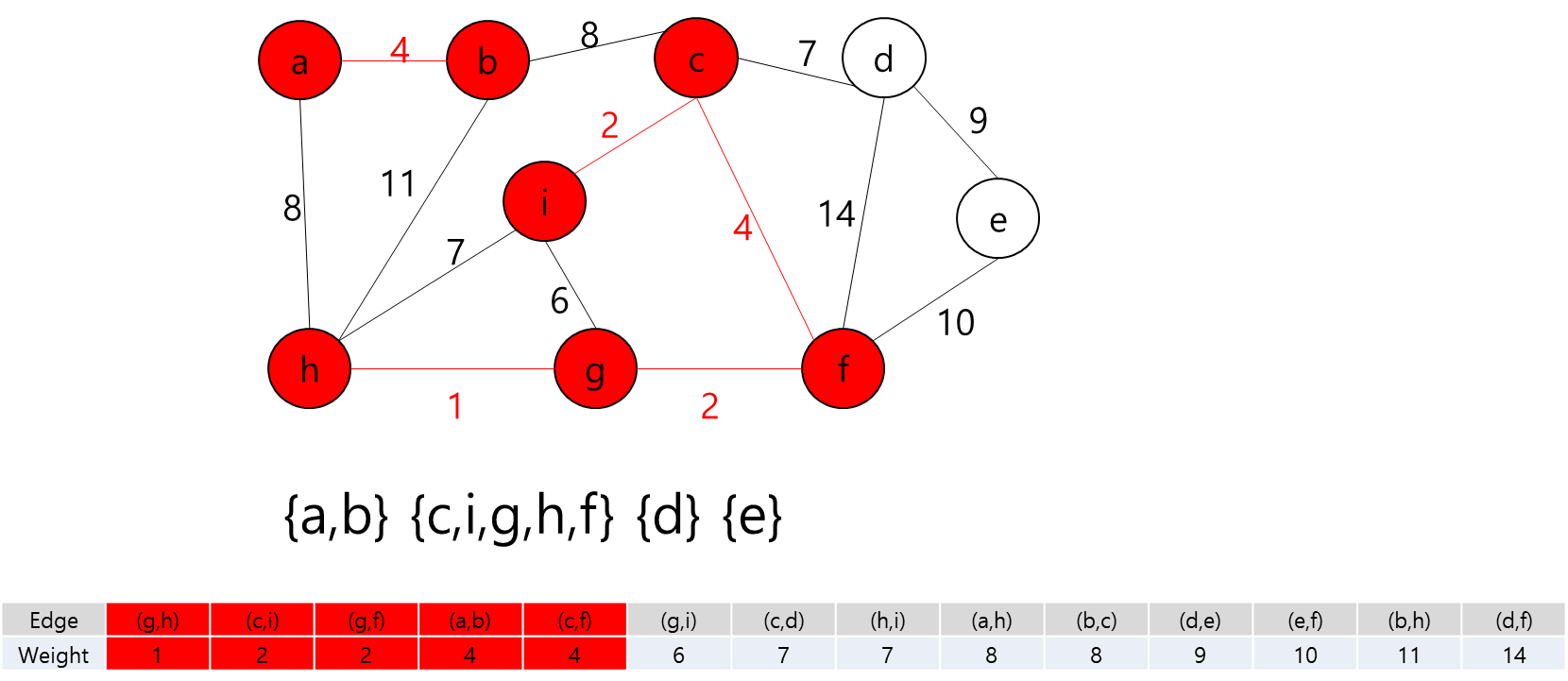
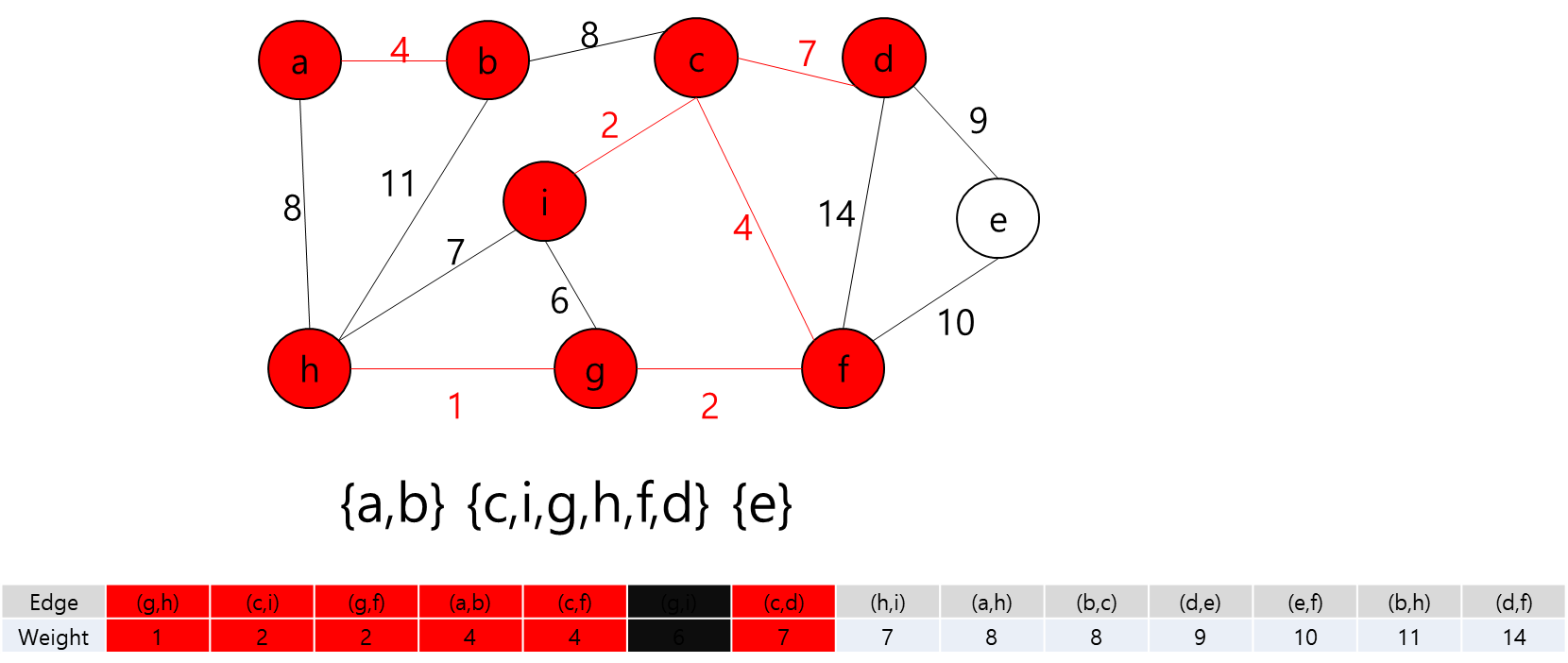
MST에 포함된 정점들(a,b,h,g,f)과 그렇지 않은 정점들을 잇는 간선 중 가중치가 가장 작은 간선((c,f))를 MST에 추가
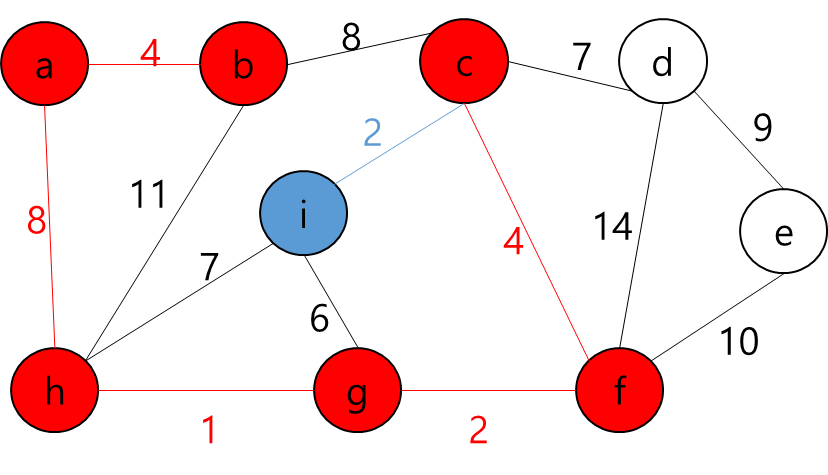
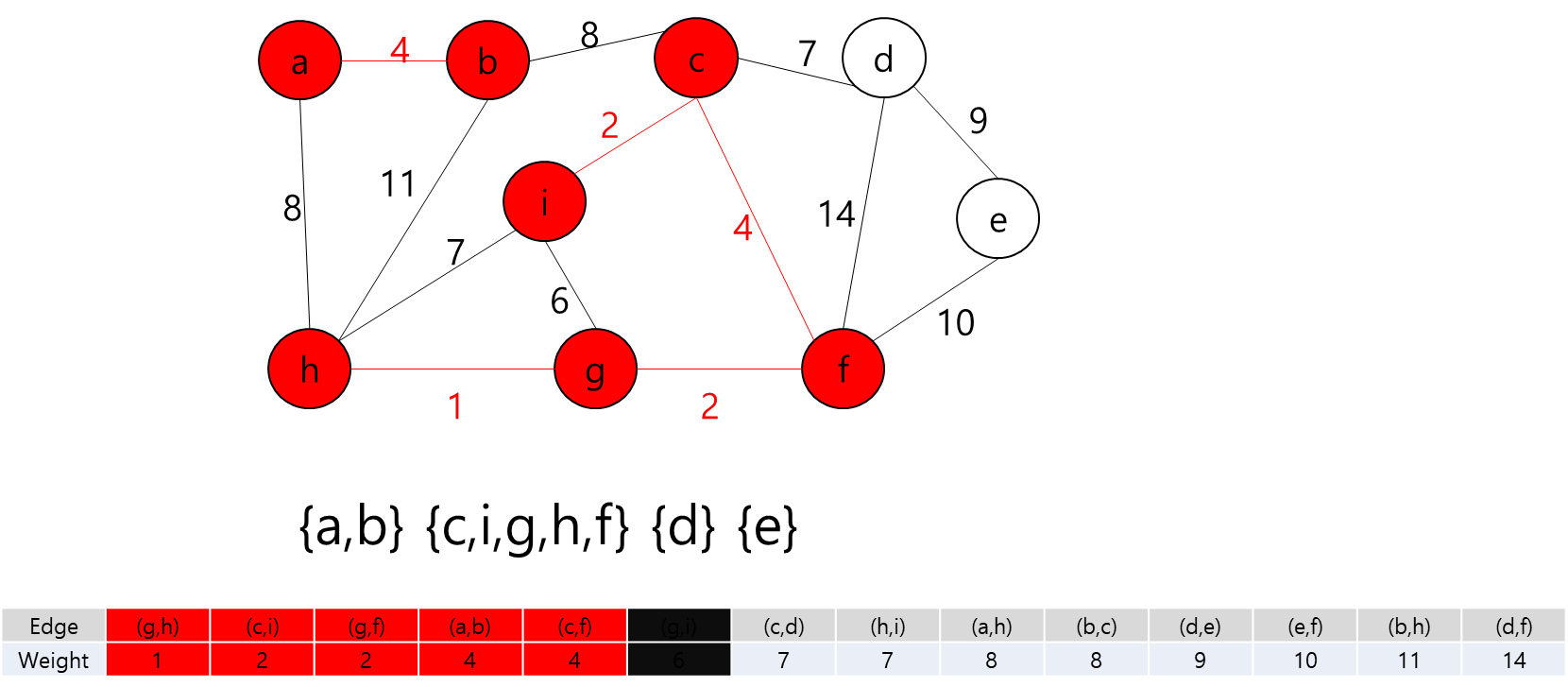
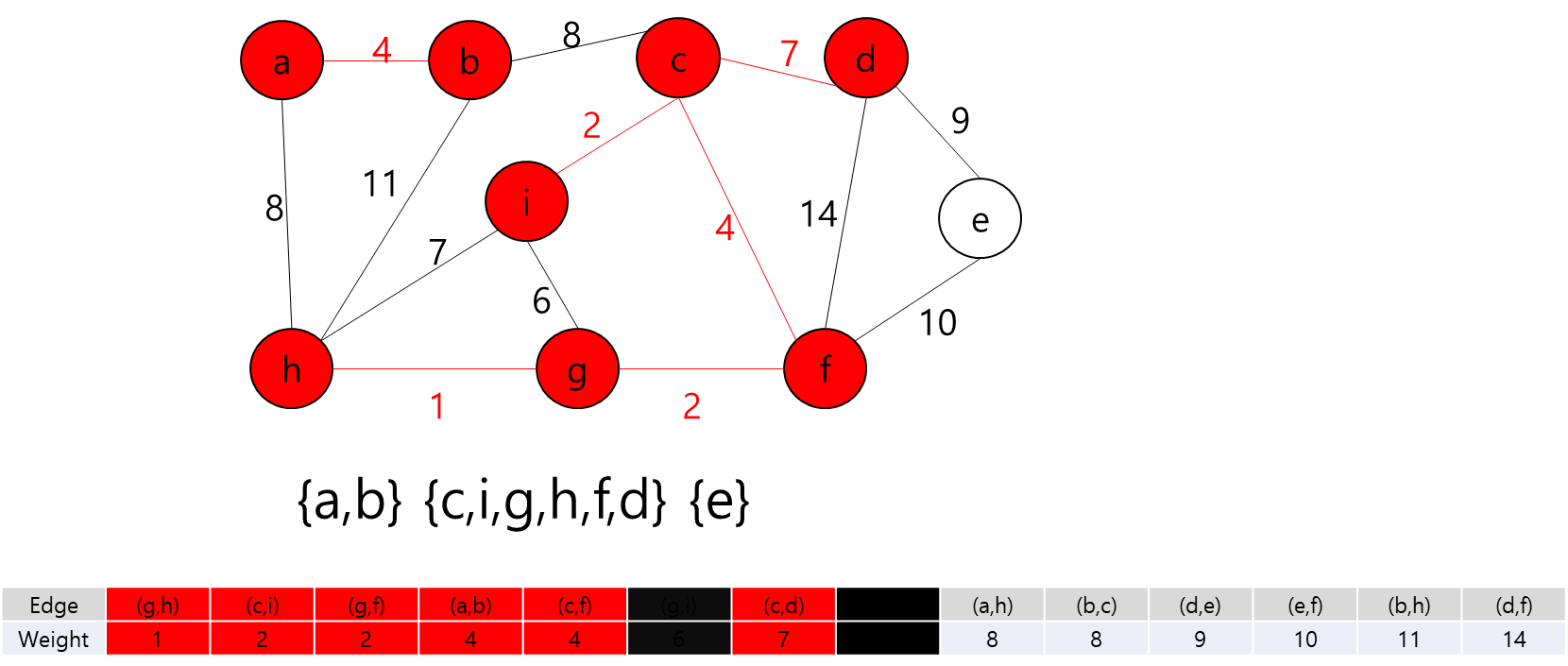
MST에 포함된 정점들(a,b,h,g,f,c)과 그렇지 않은 정점들을 잇는 간선 중 가중치가 가장 작은 간선((c,i))를 MST에 추가
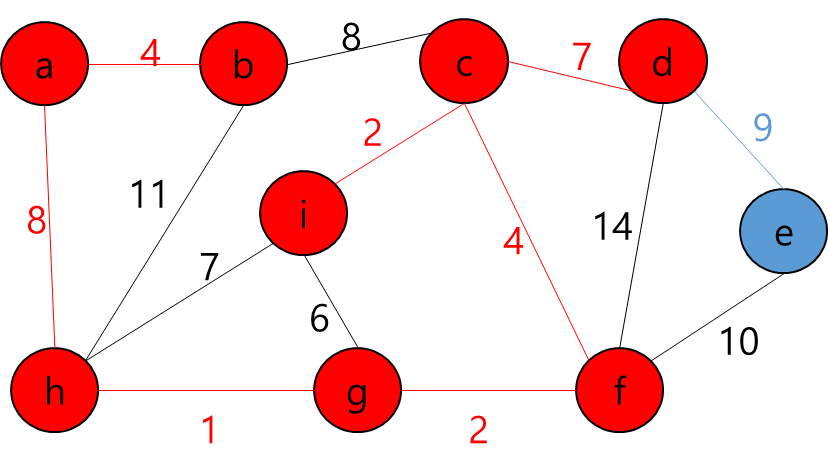
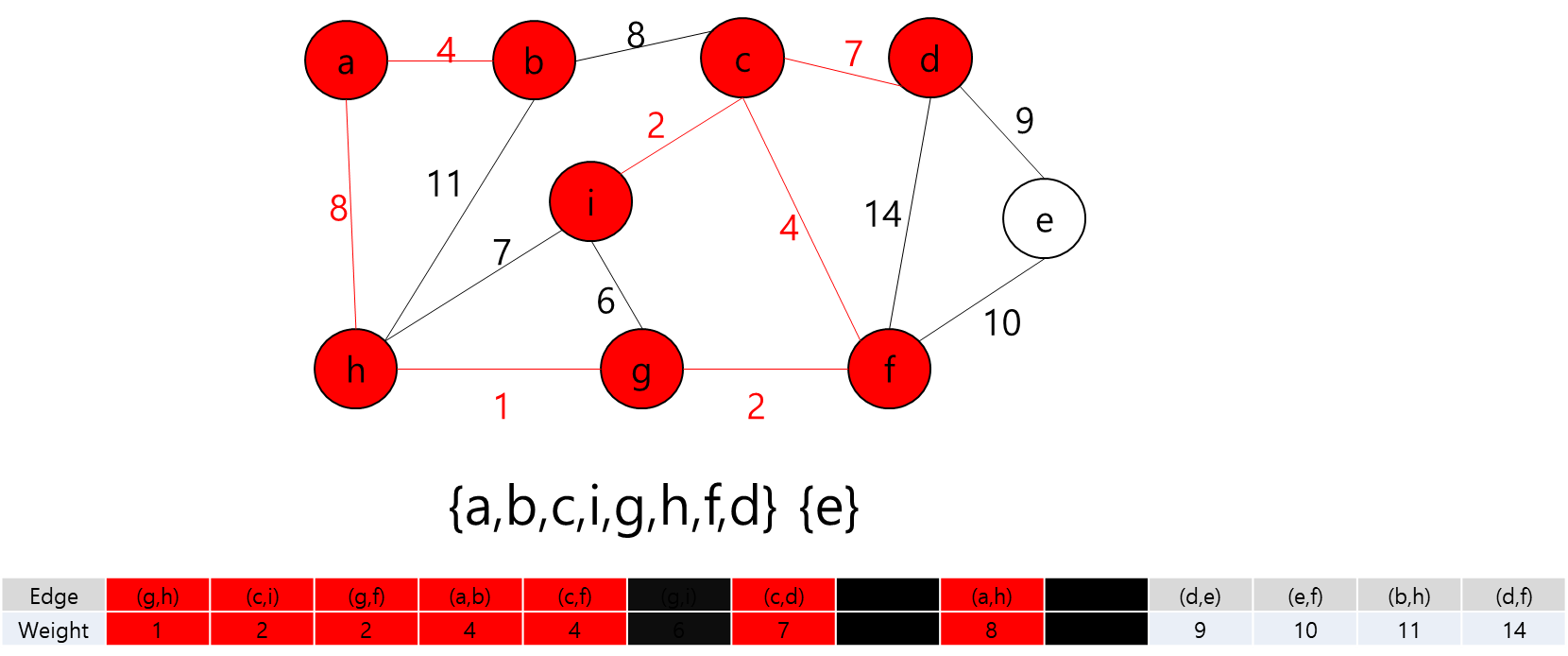
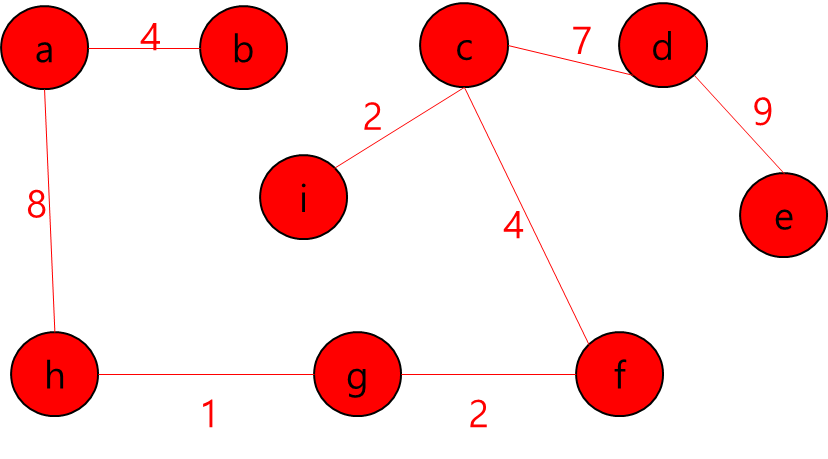
MST에 포함된 정점들(a,b,h,g,f,c,i)과 그렇지 않은 정점들을 잇는 간선 중 가중치가 가장 작은 간선((d,e))를 MST에 추가
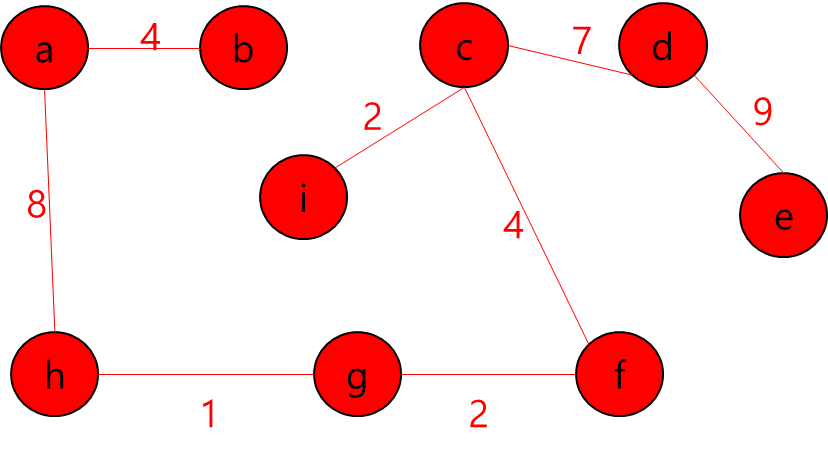
모든 정점들이 MST에 포함되어 있고 간선의 개수가 정점 개수 - 1 이므로 끝
시간 복잡도
간선의 가중치가 최소인 간선 탐색:
MST에 포함된 정점과 그렇지 않은 정점들 사이의 거리 갱신:
이것을 정점의 수 만큼 반복하므로
그러나 우선순위 큐(Priority Queue)를 사용하는 경우에는
코드
class MSTPrim {
int[][] graph;
public MSTPrim() {
this.graph = {
{0, 4, 0, 0, 0, 0, 0, 8, 0},
{4, 0, 8, 0, 0, 0, 0, 11, 0},
{0, 8, 0, 7, 0, 4, 0, 0, 7},
{0, 0, 7, 0, 9, 14, 0, 0, 0},
{0, 0, 0, 9, 10, 0, 0, 0, 0},
{0, 0, 4, 14, 10, 0, 2, 0, 0},
{0, 0, 0, 0, 0, 2, 0, 1, 7},
{8, 11, 0, 0, 0, 0, 1, 0, 7},
{0, 0, 2, 0, 0, 0, 6, 7, 0},
};
}
public int prim(startVertex) {
int vertexCount = graph.length;
int[] distance = new int[vertexCount];
boolean[] visit = new boolean[vertexCount];
Arrays.fill(distance, Integer.MAX_VALUE);
int result = 0;
distance[startVertex] = 0;
for(int i = 0; i < vertexCount; i++) {
int minDistanceFromMst = Integer.MAX_VALUE;
int targetVertex = -1;
for(int j = 0; j < vertexCount; j++) {
if(!visit[j] && distance[j] < minDistanceFromMst) {
minDistanceFromMst = distance[j];
targetVertex = j;
}
}
visit[targetVertex] = true;
result += minDistanceFromMst;
for(int j = 0; j < vertexCount; j++) {
if(!visit[j] && graph[targetVertex][j] > 0 && graph[targetVertex][j] < distance[j]) {
distance[j] = graph[targetVertex][j];
}
}
}
return result;
}
public int prim_using_priority_queue(startVertex) {
int vertexCount = graph.length;
boolean[] visit = new boolean[vertexCount];
// int[] -> {destination, weight}
PriorityQueue<int[]> queue = new PriorityQueue<>(Comparator.comparingInt(x -> x[1]);
queue.add(new int[]{startVertex, 0})
int result = 0;
while(!queue.isEmpty()) {
int[] current = queue.poll();
int destination = current[0];
int weight = current[1];
if(visit[destination]) {
continue;
}
visit[destination] = true;
result += weight;
for(int i = 0; i < vertexCount; i++) {
if(!visit[i] && graph[destination][i] > 0) {
queue.add(new int[]{i, graph[destination][i]};
}
}
}
return result;
}
}
같이 볼 자료
2022.01.16 - [Algorithm] - [Algorithm] MST (Minimum Spanning Tree, 최소 신장 트리)
[Algorithm] MST (Minimum Spanning Tree, 최소 신장 트리)
신장 트리 (Spanning Tree) 그래프의 모든 정점을 연결하는 트리 트리: 일반적으로 계층구조의 자료구조를 생각하는데, 그래프 이론에서 사이클이 없는 무방향 그래프를 트리라고 한다. 그래프가 n
jino-dev-diary.tistory.com
2022.01.16 - [Algorithm] - [Algorithm] Krsukal (크루스칼) 알고리즘
[Algorithm] Krsukal (크루스칼) 알고리즘
Kruskal (크루스칼) 알고리즘 그래프의 모든 정점을 최소 비용으로 연결하는, 즉, 최소 신장 트리를 구현하는 대표적인 Greedy(탐욕) 알고리즘이다. Greedy 알고리즘 그 순간에 가장 좋다고 생각되는
jino-dev-diary.tistory.com
'Algorithm' 카테고리의 다른 글
| [Alogorithm] Dijkstra(다익스트라) 알고리즘 (1) | 2024.01.24 |
|---|---|
| [Algorithm] 최단 경로 문제 (Shortest Path Problem) (1) | 2024.01.24 |
| [Algorithm] Krsukal (크루스칼) 알고리즘 (0) | 2022.01.16 |
| [Algorithm] MST (Minimum Spanning Tree, 최소 신장 트리) (0) | 2022.01.16 |
| [Algorithm] BFS (Breath-First-Search, 너비 우선 탐색) (0) | 2022.01.08 |
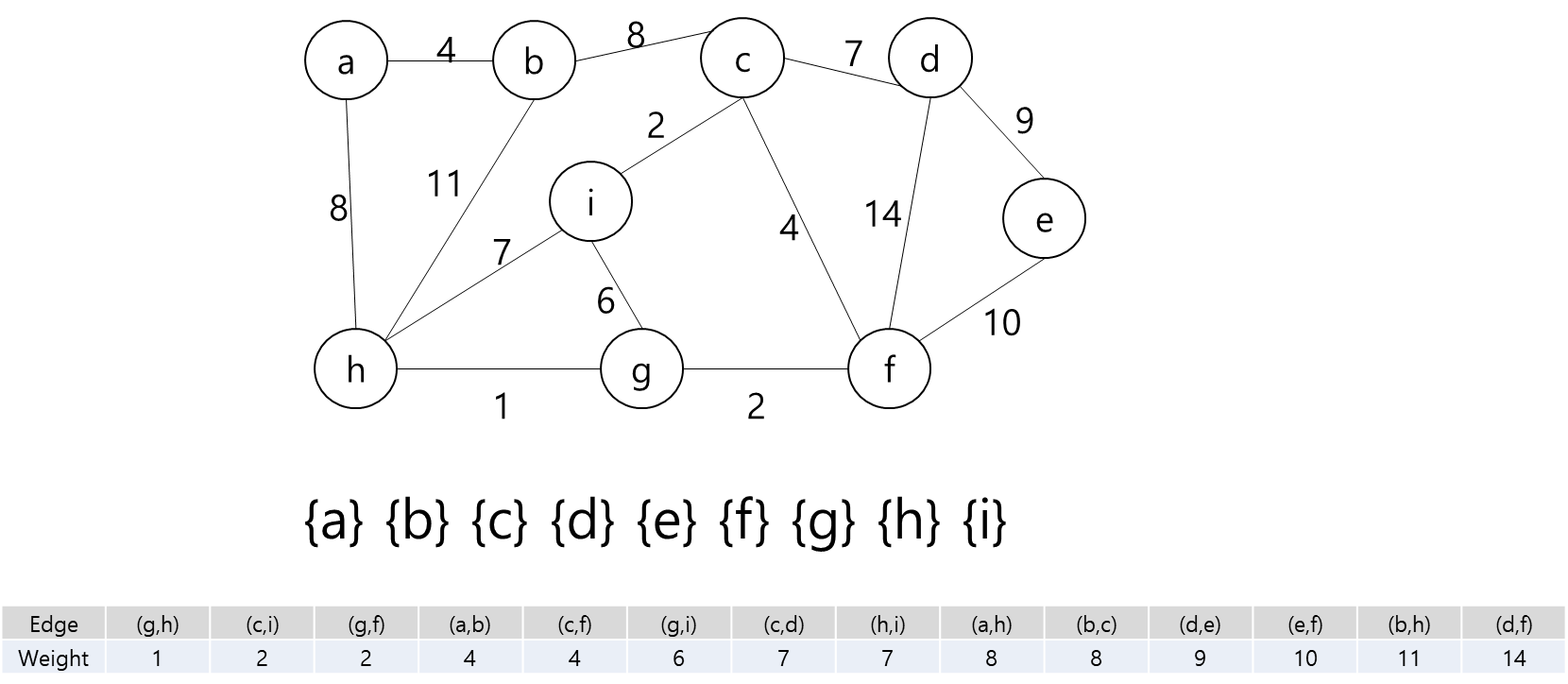
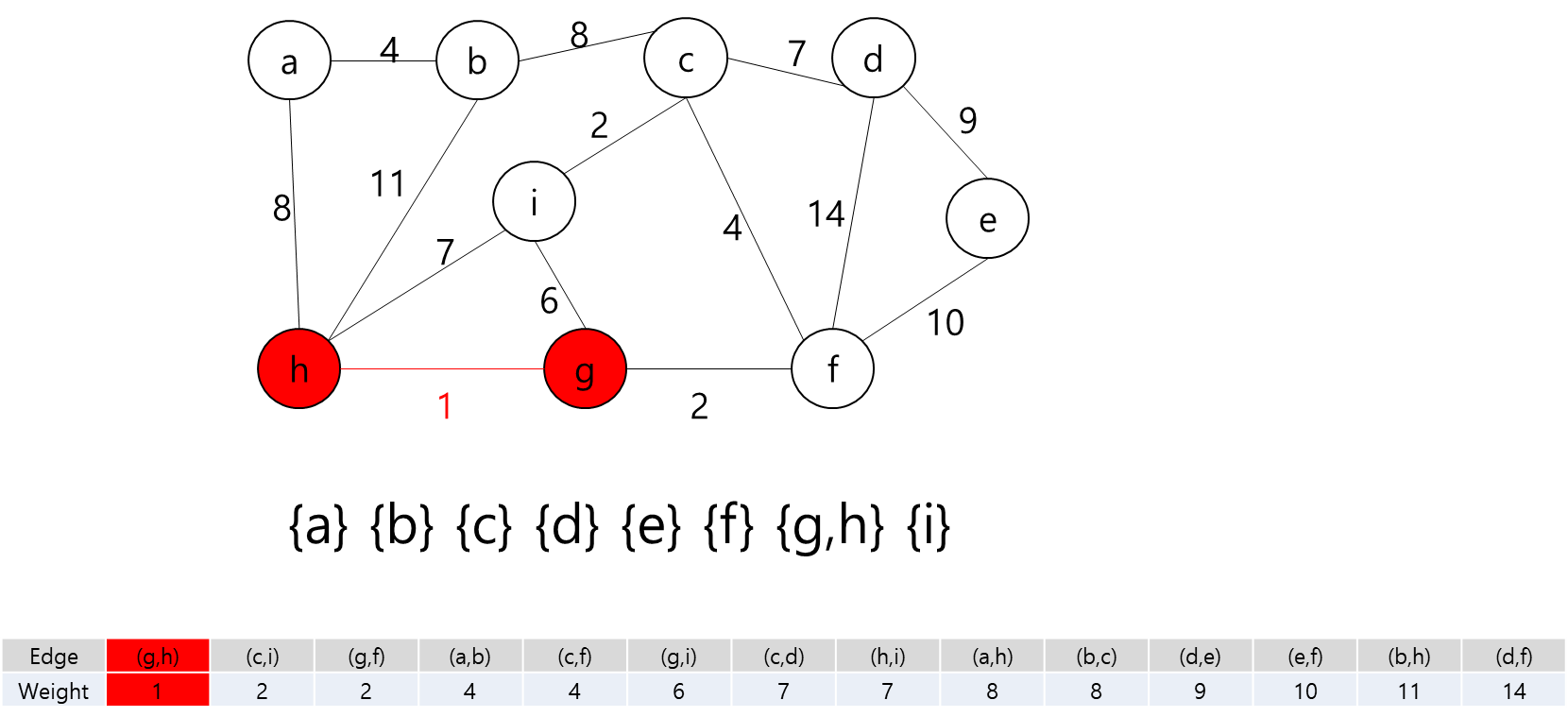


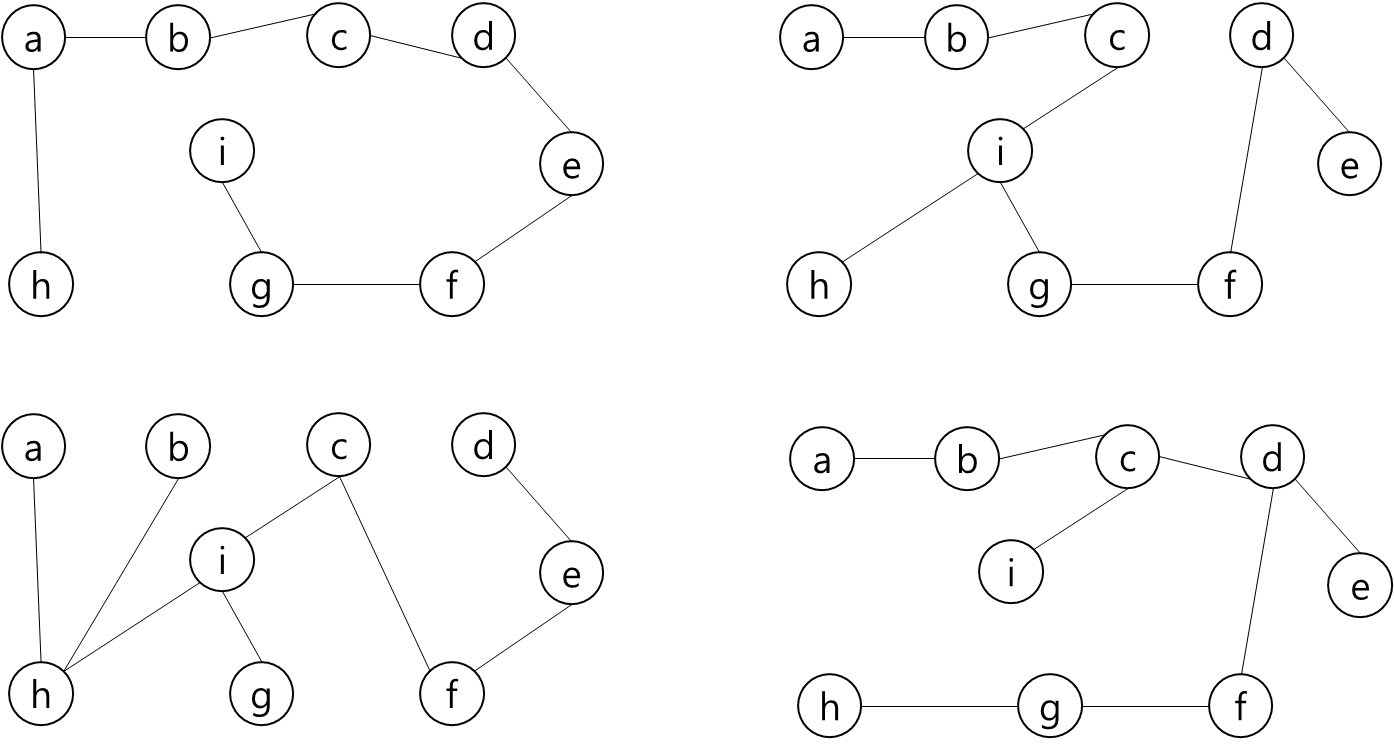








 vs
vs