Kruskal (크루스칼) 알고리즘
그래프의 모든 정점을 최소 비용으로 연결하는, 즉, 최소 신장 트리를 구현하는 대표적인 Greedy(탐욕) 알고리즘이다.
Greedy 알고리즘
- 그 순간에 가장 좋다고 생각되는 해를 선택
- 정렬 된 간선 중 가중치가 가장 작은 간선부터 차례대로 선택
- 그 순간에는 최적의 해일 수 있지만, 전체적으로 봤을때는 그렇지 않을 수 있으므로 반드시 검증을 해야함
- 이미 선택된 간선인지, 사이클을 형성하는지 검증
- Prim(프림) 알고리즘의 경우는 정점을 선택하는 Greedy 알고리즘이다.
동작방식
- 그래프의 간선들을 오름차순으로 정렬한다.
- 정렬된 간선들을 차례대로 선택한다.
- 단, 이미 선택된 간선과 사이클을 형성하는 간선은 패스
- 간선의 개수가
Visualize

처음은 어떠한 정점들도 선택되지 않은 상태, 간선들을 오름차순 정렬

정렬된 간선을 차례대로 선택하여 MST에 추가한다. 간선 (g,h)를 추가하고 정점 g,h를 같은 집합으로 합친다.

간선 (c,i)를 추가하고 정점 c와 i를 같은 집합으로 합친다.
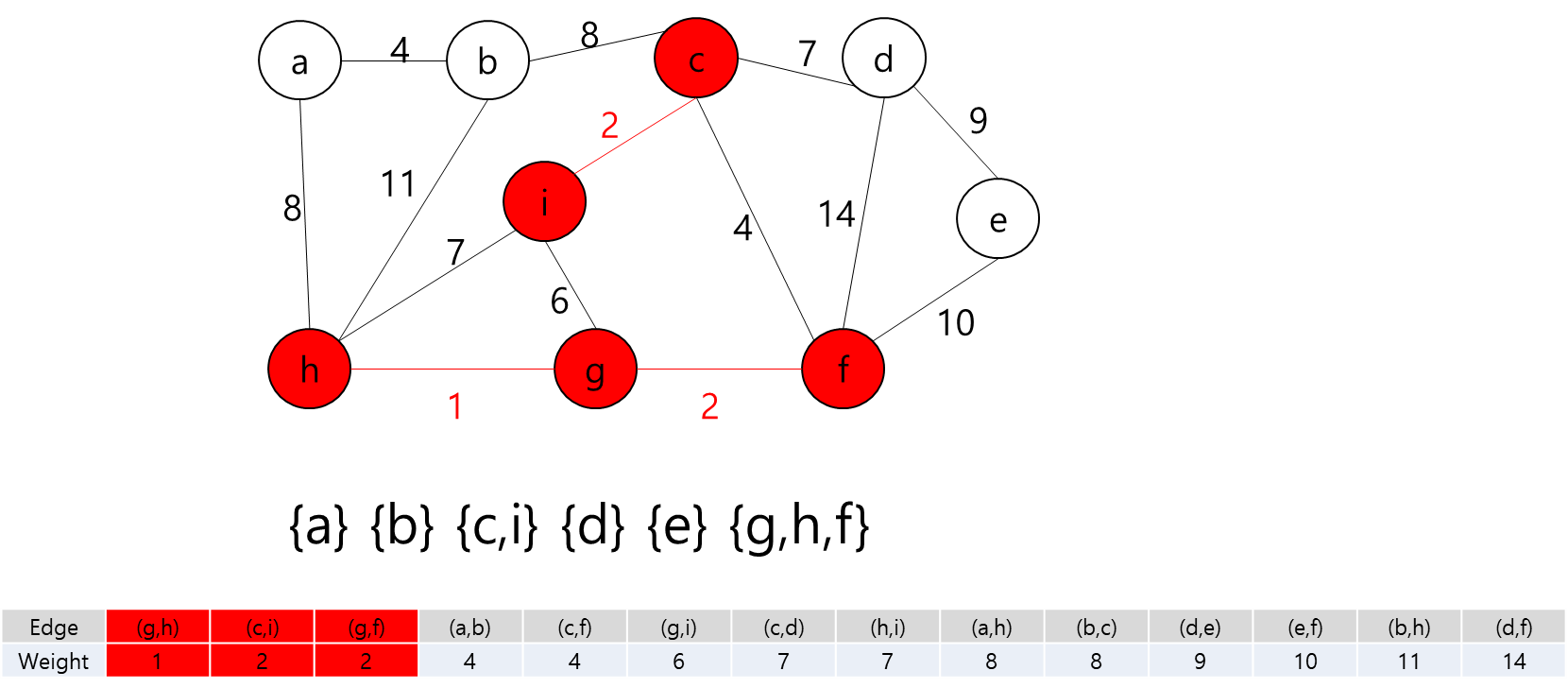
간선 (g,f)를 추가하고 정점 f와 g를 같은 집합으로 합친다.
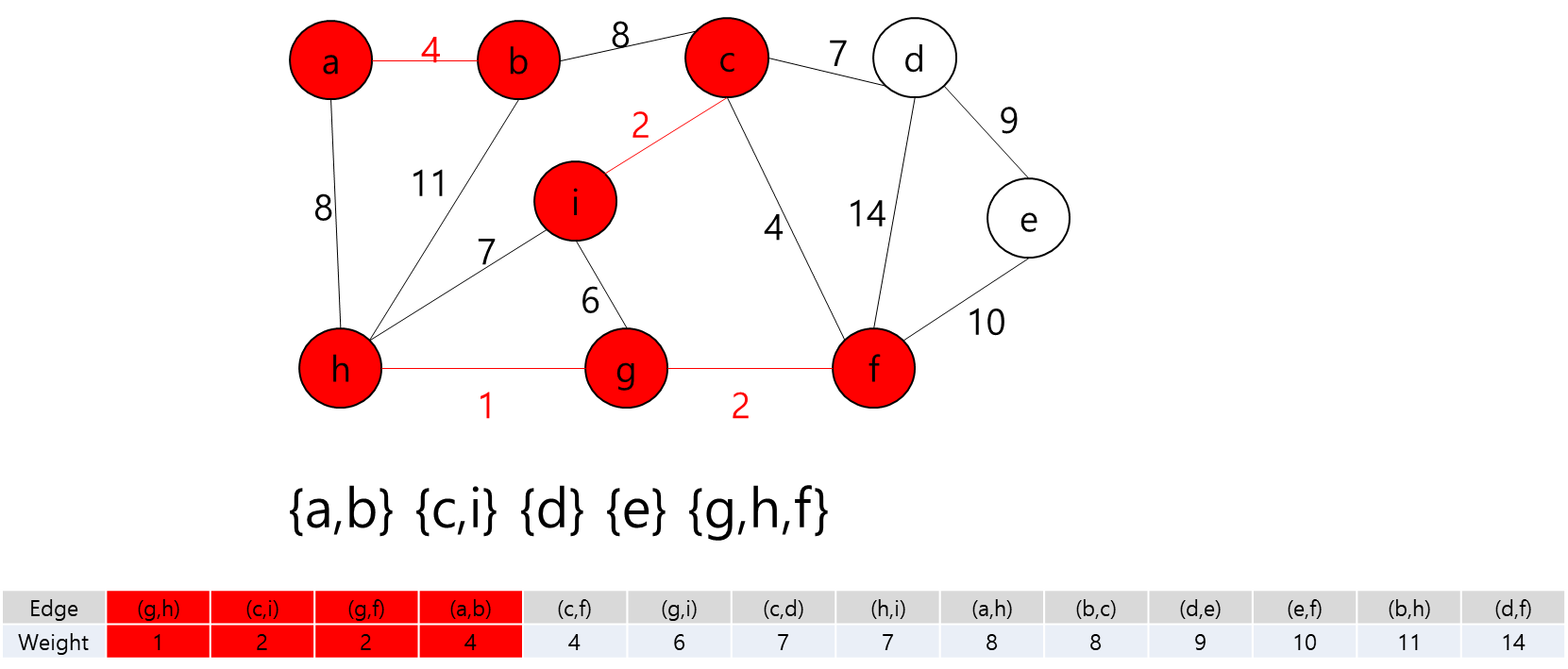
간선 (a,b)를 추가하고 정점 a와 b를 같은 집합으로 합친다.
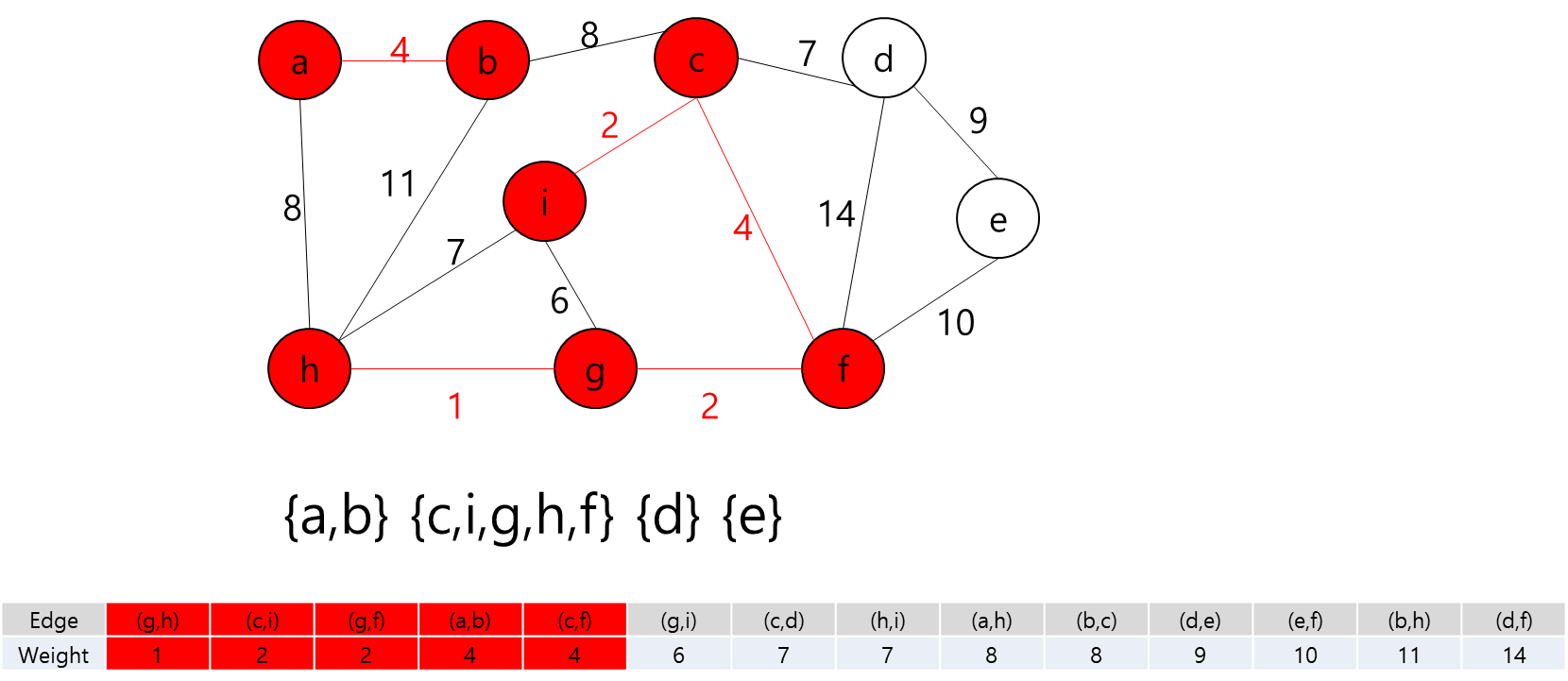
간선 (c,f)를 추가하고 정점 c와 f를 같은 집합으로 합친다.
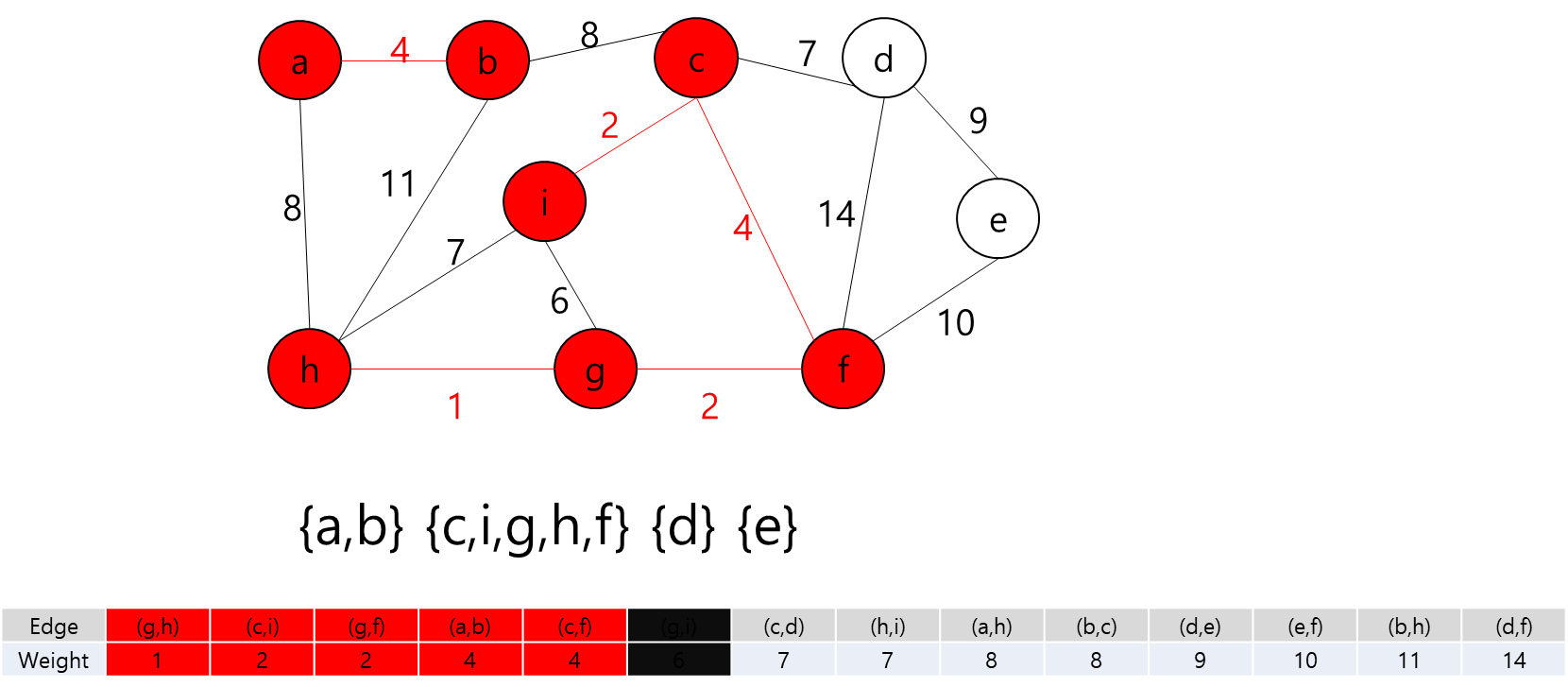
간선 (g,i)를 추가하려고 하는데.. 정점 g와 i는 이미 같은 집합이다. 만약 간선 (g,i)를 추가하면 사이클이 형성된다. 그러므로 그냥 패스
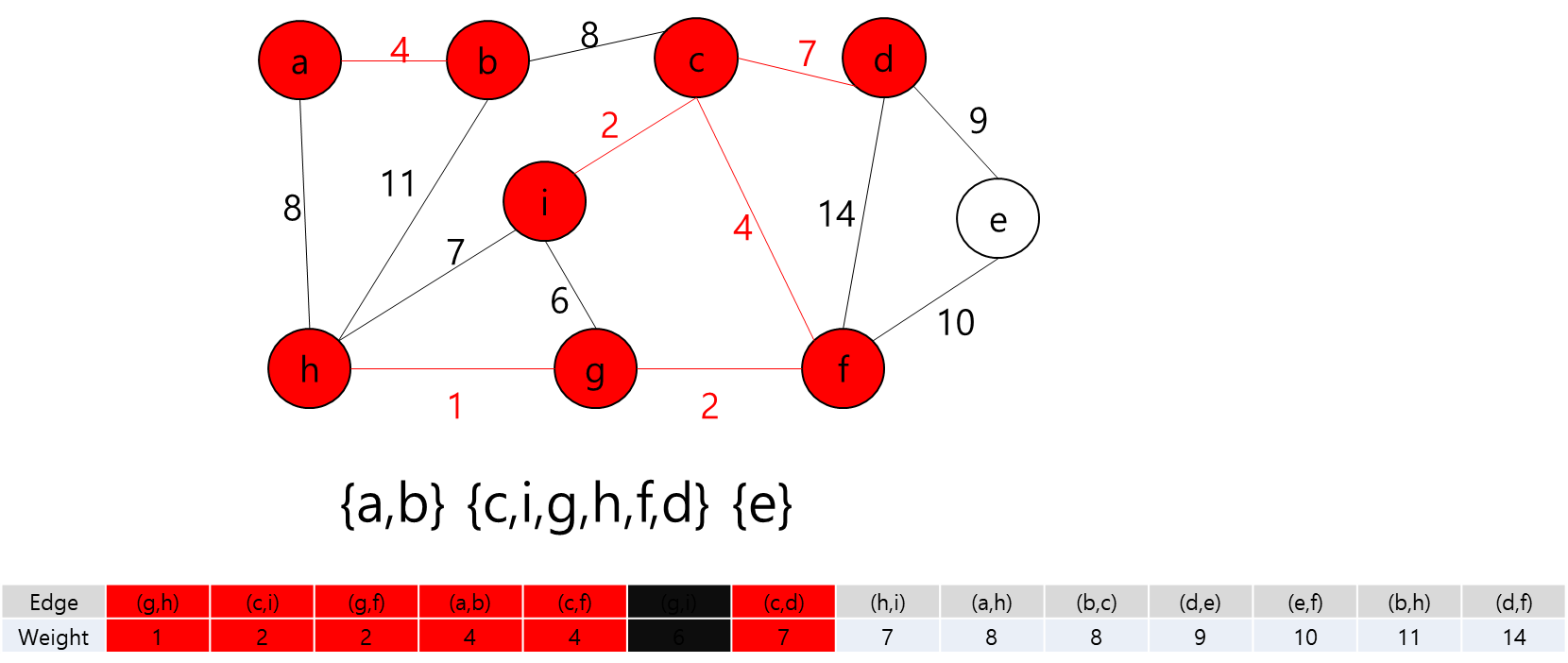
간선 (c,d)를 추가하고 정점 c와 d를 같은 집합으로 합친다.
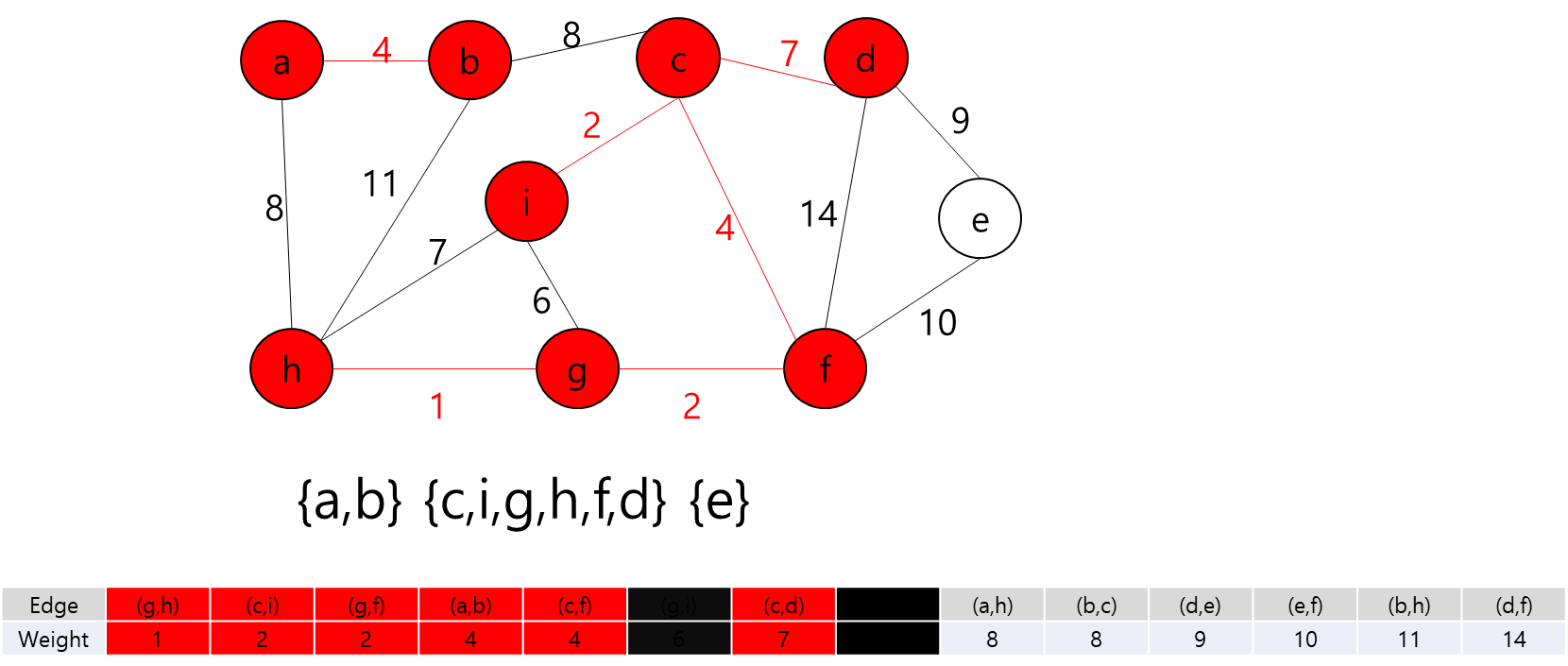
간선 (h,i)를 추가하려고 하는데.. 정점 h와 i는 이미 같은 집합이다. 만약 간선 (h,i)를 추가하면 사이클이 형성된다. 그러므로 그냥 패스
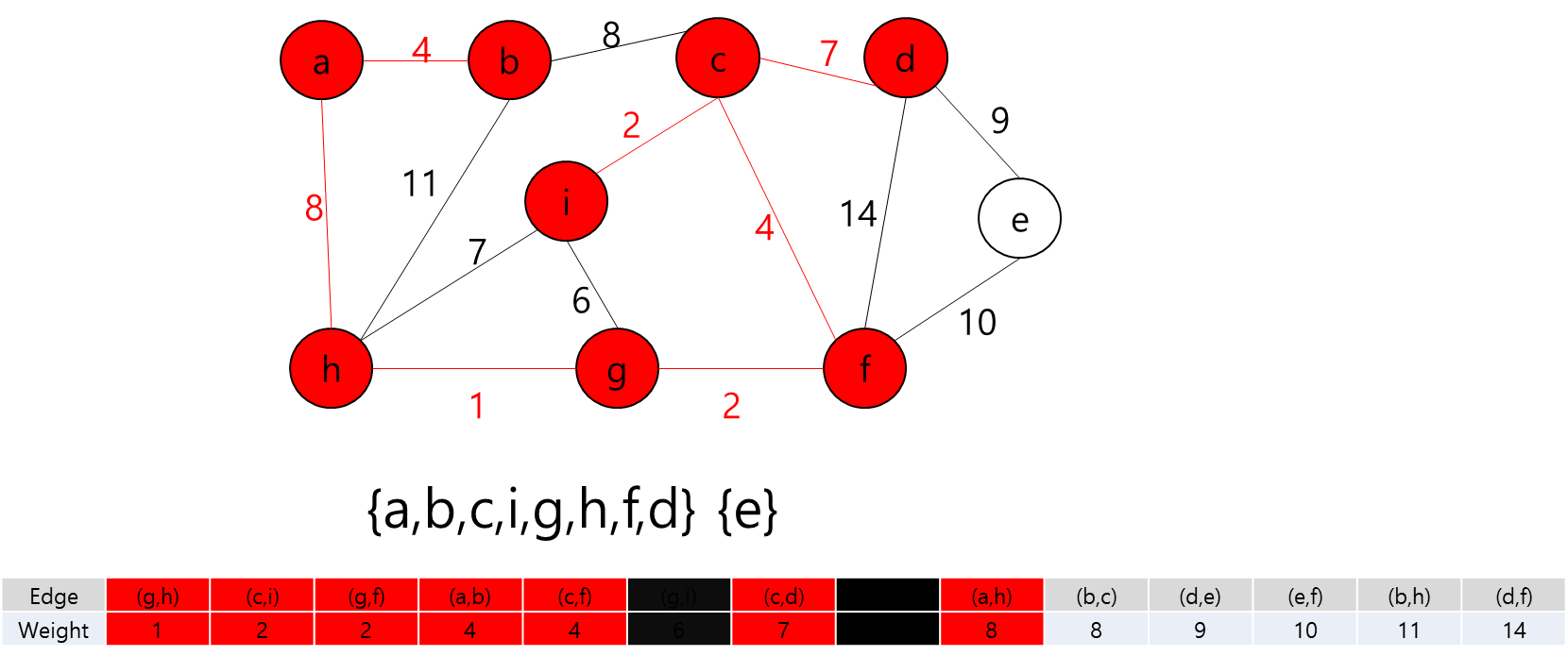
간선 (a,h)를 추가하고 a와 h를 같은 집합으로 합친다.
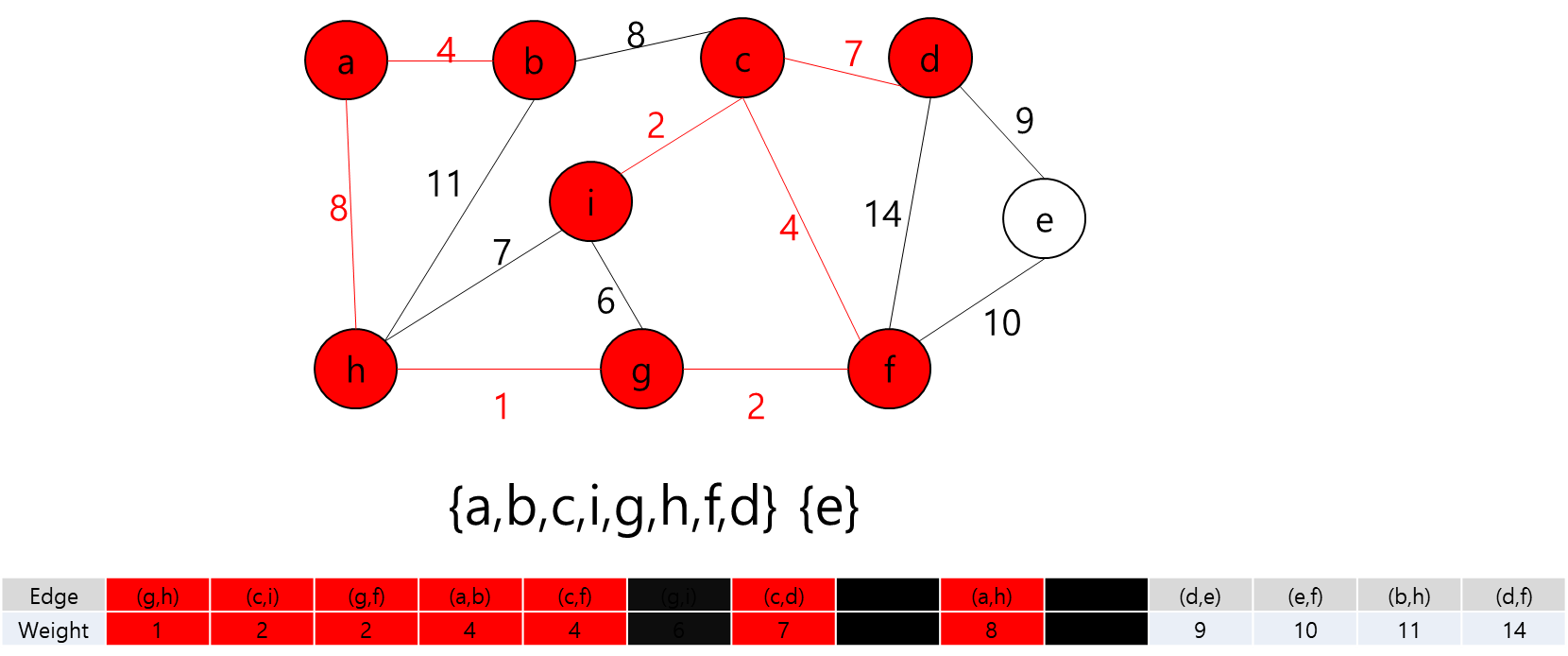
간선 (b,c)를 추가하려고 하는데... b와 c는 이미 같은 집합이다. 만약 간선 (b,c)를 추가한다면 사이클이 형성된다. 그러므로 그냥 패스
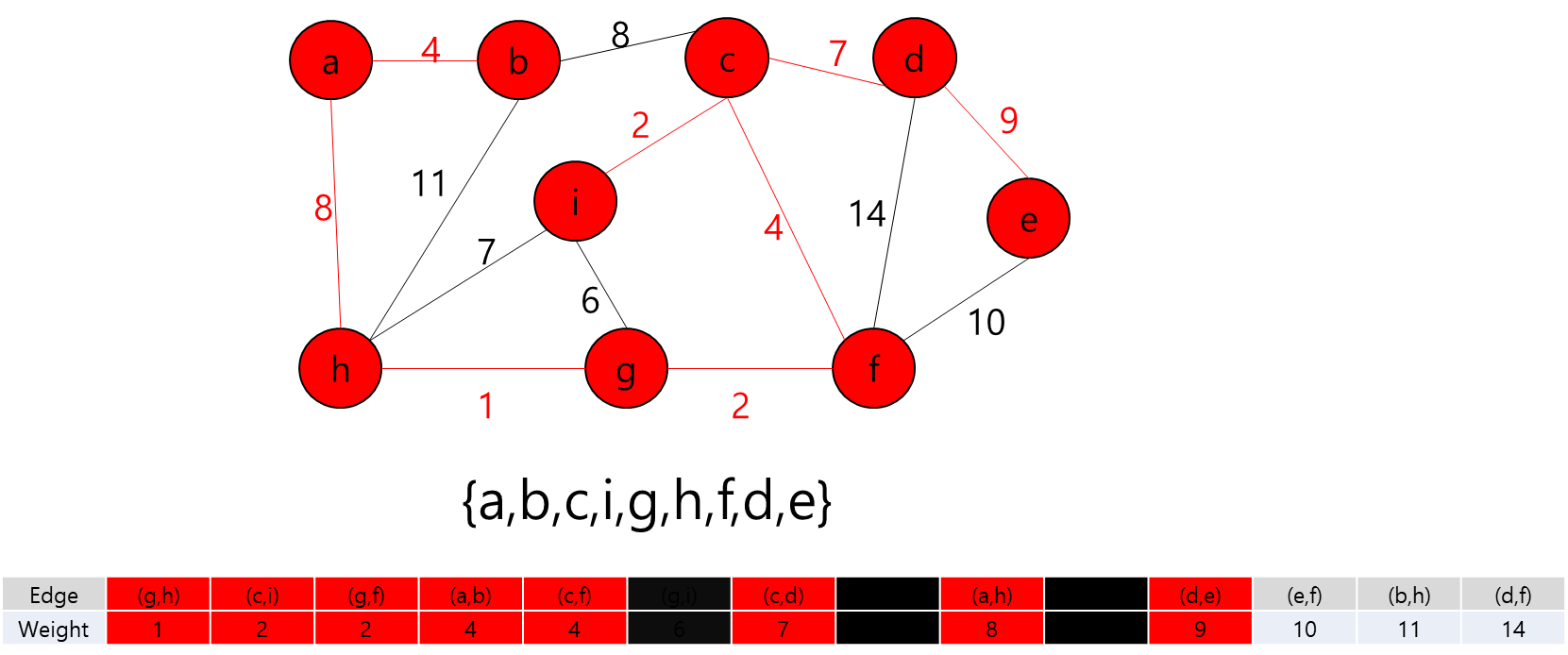
간선 (d,e)를 추가하고 정점 d와 e를 같은 집합으로 합친다.
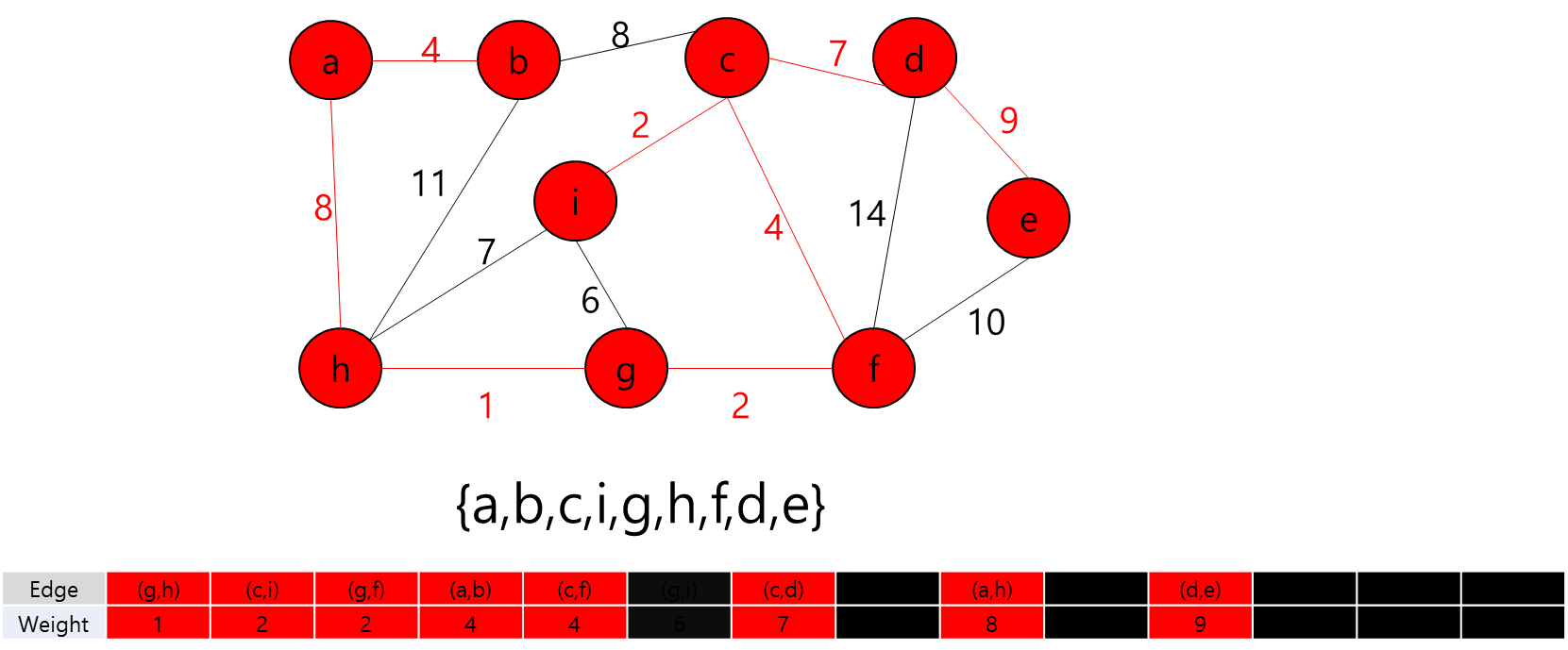
모든 정점들이 같은 집합이고, MST에 추가된 간선이 정점 개수 - 1이므로 끝
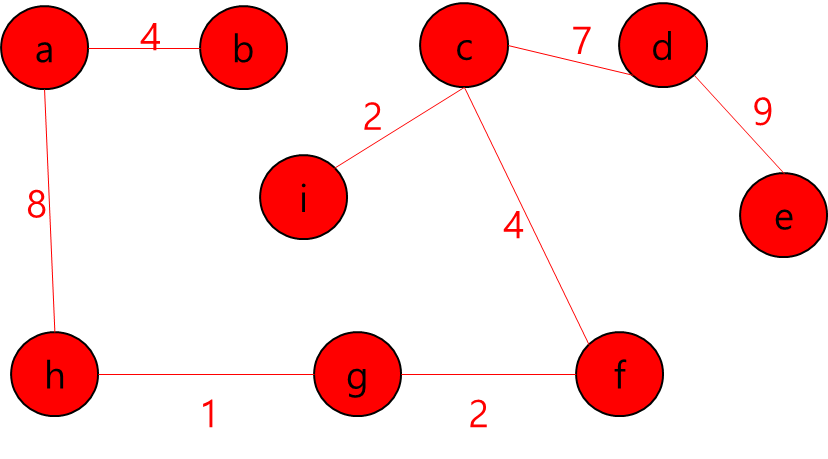
사이클을 형성하는 지 검증할 때 Union-Find 알고리즘을 사용한다
시간복잡도
Union-Find 알고리즘을 사용하면 간선들을 정렬하는 시간에 영향받는다.
즉, 간선
코드
class MSTKruskal {
int[] parents;
int[][] graph;
public MSTKruskal() {
this.graph = {
{0, 4, 0, 0, 0, 0, 0, 8, 0},
{4, 0, 8, 0, 0, 0, 0, 11, 0},
{0, 8, 0, 7, 0, 4, 0, 0, 7},
{0, 0, 7, 0, 9, 14, 0, 0, 0},
{0, 0, 0, 9, 10, 0, 0, 0, 0},
{0, 0, 4, 14, 10, 0, 2, 0, 0},
{0, 0, 0, 0, 0, 2, 0, 1, 7},
{8, 11, 0, 0, 0, 0, 1, 0, 7},
{0, 0, 2, 0, 0, 0, 6, 7, 0},
}
}
public int kruskal() {
int[][] edges = buildEdges();
makeSet();
int result = 0;
for(int i = 0; i < edges.lengh; i++) {
int source = edges[i][0];
int destination = edges[i][1];
int weight = edges[i][2];
if(find(source) != find(destination)) {
union(source, destination);
result += weight;
}
}
return result;
}
public int[][] buildEdges() {
int[][] edges = new int[][]{};
index = 0;
for(int i = 0; i < graph.length; i++) {
for(int j = 0; j < graph.length; j++) {
if(graph[i][j] !=0) {
edges[index++] = {i, j, graph[i][j]};
edges[index++] = {j, i, graph[j][i]};
}
}
}
return edges;
}
public void makeSet() {
this.parents = new int[graph.length];
for(int i = 0; i < graph.lenght; i++) {
parents[i] = i;
}
}
public int find(x) {
if(parents[x] == x) {
return x;
}
return parents[x] = find(parents[x]);
}
public int union(x, y) {
x = find(x);
y = find(y);
if(x == y) {
return;
}
if(x > y) {
parents[y] = x;
} else {
parents[x] = y;
}
}
}
같이 볼 자료
2022.01.16 - [Algorithm] - [Algorithm] MST (Minimum Spanning Tree, 최소 신장 트리)
[Algorithm] MST (Minimum Spanning Tree, 최소 신장 트리)
신장 트리 (Spanning Tree) 그래프의 모든 정점을 연결하는 트리 트리: 일반적으로 계층구조의 자료구조를 생각하는데, 그래프 이론에서 사이클이 없는 무방향 그래프를 트리라고 한다. 그래프가 n
jino-dev-diary.tistory.com
2022.01.16 - [Algorithm] - [Algorithm] Prim(프림) 알고리즘
[Algorithm] Prim(프림) 알고리즘
Prim(프림) 알고리즘 그래프의 모든 정점을 최소 비용으로 연결하는, 즉, 최소 신장 트리를 구현하는 대표적인 Greedy(탐욕) 알고리즘이다. Greedy 알고리즘 그 순간에 가장 좋다고 생각되는 해를 선
jino-dev-diary.tistory.com
'Algorithm' 카테고리의 다른 글
| [Algorithm] 최단 경로 문제 (Shortest Path Problem) (1) | 2024.01.24 |
|---|---|
| [Algorithm] Prim(프림) 알고리즘 (0) | 2022.01.16 |
| [Algorithm] MST (Minimum Spanning Tree, 최소 신장 트리) (0) | 2022.01.16 |
| [Algorithm] BFS (Breath-First-Search, 너비 우선 탐색) (0) | 2022.01.08 |
| [Algorithm] DFS (Depth-First-Search, 깊이 우선 탐색) (0) | 2022.01.08 |