참고1 : 유튜브 (권오흠 교수, 2015 봄학기 알고리즘)
참고2 : (다양한 예제로 학습하는) 데이터 구조와 알고리즘 for java
1. 그래프 : G = (V, E)
1. 정의
- V : 정점(Vertex) 또는 노드(Node)들의 집합
- E : 간선,에지(Edge) 또는 링크(Link)라고 불리는 정점들의 쌍의 집합
- G = (V, E)
2. 종류
- 무방향(undirected) 그래프 vs 방향(directed) 그래프
- 방향이 없는 그래프 vs 방향이 있는 그래프
- (u, v) == (v, u) vs (u, v) != (v,u)
 vs
vs 
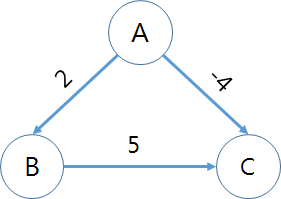
- 가중치 그래프(Weight Graph)
- 방향, 무방향 그래프에 관계없이 각 간선에 가중치(weight) 혹은 비용(cost)이 할당된 그래프
3. 용어
- 인접 정점 or 인접 노드 : 간선에 의해 연결된 정점
- 차수(degree) : 정점에 연결된 다른 정점의 개수
- 진입 차수(in-degree) : 방향 그래프에서 외부 노드에서 들어오는 간선의 수
- 진출 차수(out-degree) : 방향 그래프에서 외부 노드로 나가는 간선의 수
- 연결 그래프(connected Graph)
- 무방향 그래프에서 두 노드 사이를 연결하는 경로(path)가 존재할 때 두 정점은 서로 연결되어 있다고 한다.
- 그래프 안의 모든 정점이 연결되어 있을때 연결된 그래프라고 한다
- 연결 요소

{a,b,c,d}, {e,f}, {g,h,i}로 3개이다.
2. 그래프의 표현
1. 인접 행렬

인접 행렬 (무방향 그래프) - 두 정점 사이에 간선이 있을경우 1, 없을 경우 0으로 표현한다.
- 가중치 그래프의 경우 0,1 대신 가중치로 표현한다.
- 무방향 그래프의 경우 자기 자신을 기준으로 대칭이다. (A, B) == (B, A)
- 방향 그래프의 경우 비대칭이다.
- 저장공간 : O(n^2)
- 어떤 노드 v에 인접한 모든 노드를 찾을 때 걸리는 시간 : O(n)
- 어떤 간선 (u,v)가 존재하는지 검사할때 걸리는 시간 : O(1)
- 두 정점 사이에 간선이 있을경우 1, 없을 경우 0으로 표현한다.
- 간단한 구현 코드 (무방향 그래프)
public class Graph {
int[][] adjMatrix;
int vertexCount;
public Graph(int count) {
vertexCount = count;
adjMatrix = new int[vertexCount][vertexCount];
}
public void addEdge(int u, int v) {
adjMatrix[u][v] = 1;
adjMatrix[v][u] = 1;
}
public void removeEdge(int u, int v) {
adjMatrix[u][v] = 0;
adjMatrix[v][u] = 0;
}
public List<Integer> findAdjVertex(int u) {
ArrayList<Integer> adjVertexList = new ArrayList<>();
for(int i = 0; i<adjMatrix.length; i++) {
if(adjMatrix[u][i] == 1) {
adjVertexList.add(i);
}
}
return adjVertexList;
}
public boolean isEdge(int u, int v) {
return adjMatrix[u][v] == 1;
}
}
2. 인접 리스트

인접 리스트 (무방향 그래프) - 정점 집합을 표현하는 하나의 배열과 각 정점마다 인접한 정점들의 리스트
- 두 정점 사이에 간선이 있을 경우 리스트에 추가한다 (순서는 상관없다)
- 저장 공간 : O(n+m)
- n은 정점개수, m은 간선 개수이다.
- 무방향 그래프의 경우 2m, 방향 그래프의 경우 m이지만, Big - O 표기법에서는 O(n+m)이다.
- 어떤 노드 v에 인접한 모든 노드를 찾을 때 걸리는 시간 : O(degree(v))
- v에 해당하는 리스트의 길이이다.
- 어떤 간선 (u,v)가 존재하는지 검사할 때 걸리는 시간 : O(degree(u))
- u에 대한 연결 리스트를 돌면서 v가 있는지 확인한다.
- 간단한 구현코드 (무방향 그래프)
public class Graph {
List<Integer>[] adjList;
int vertexCount;
public Graph(int count) {
vertexCount = count;
adjList = new List[vertexCount];
for(int i = 0; i<vertexCount; i++) {
adjList[i] = new ArrayList<>();
}
}
public addEdge(int u, int v) {
adjList[u].add(v);
adjList[v].add(u);
}
public removeEdge(int u, int v) {
adjList[u].remove(adjList[u].indexOf(v));
adjList[v].remove(adjList[v].indexOf(u));
}
public List<Integer> findAdjVertex(int u) {
return adjList[u];
}
public boolean isEdge(int u, int v) {
for(int i = 0; i < adjList[u].size(); i++) {
if(adjList[u].get(i) == v) {
return true;
}
}
return false;
}
}'Algorithm' 카테고리의 다른 글
| [Algorithm] 정렬 - Insertion Sort (삽입 정렬) (0) | 2021.09.15 |
|---|---|
| [Algorithm] 정렬 - Bubble Sort (거품 정렬) (0) | 2021.09.13 |
| [Algorithm] 정렬 - Selection Sort (선택 정렬) (0) | 2021.09.13 |
| [Algorithm] 문장의 유사도 분석 - 편집 거리 알고리즘 (Levenshtein Distance) (0) | 2021.01.20 |
| [Algorithm] Dynamic Programming - Longest Common Sequence(LCS) (0) | 2020.11.12 |