Dev 일기장

# 개요

벨만 포드 알고리즘 정리

용어가 좀 혼용될 수 있다

• Ex) 노드 == 정점, 간선 == 엣지

예시 그림을 다익스트라와 같은걸로 하다보니 좀 짧다 (더 좋은 예시 있으면 수정 할 예정)

# 벨만 포드 알고리즘

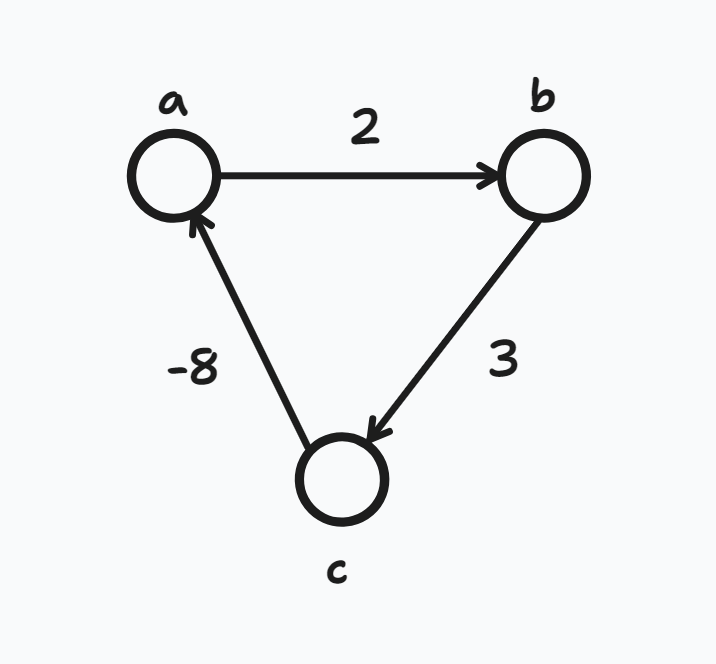
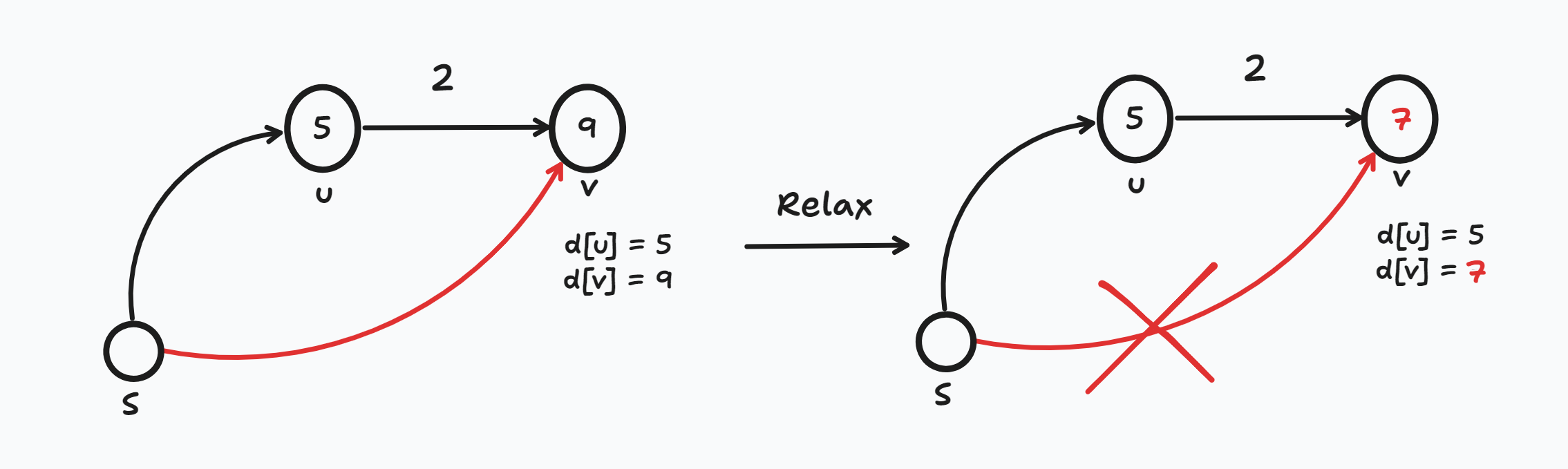
음수 사이클이 없는 그래프에서 한 정점에서 다른 모든 정점까지의 최단 경로 및 거리를 구하는 알고리즘

Dijkstra 알고리즘과의 차이

• 음수 간선이 있는 경우에도 구할 수 있다.
• Dijkstra 알고리즘 보다 느리다.

# 동작 과정

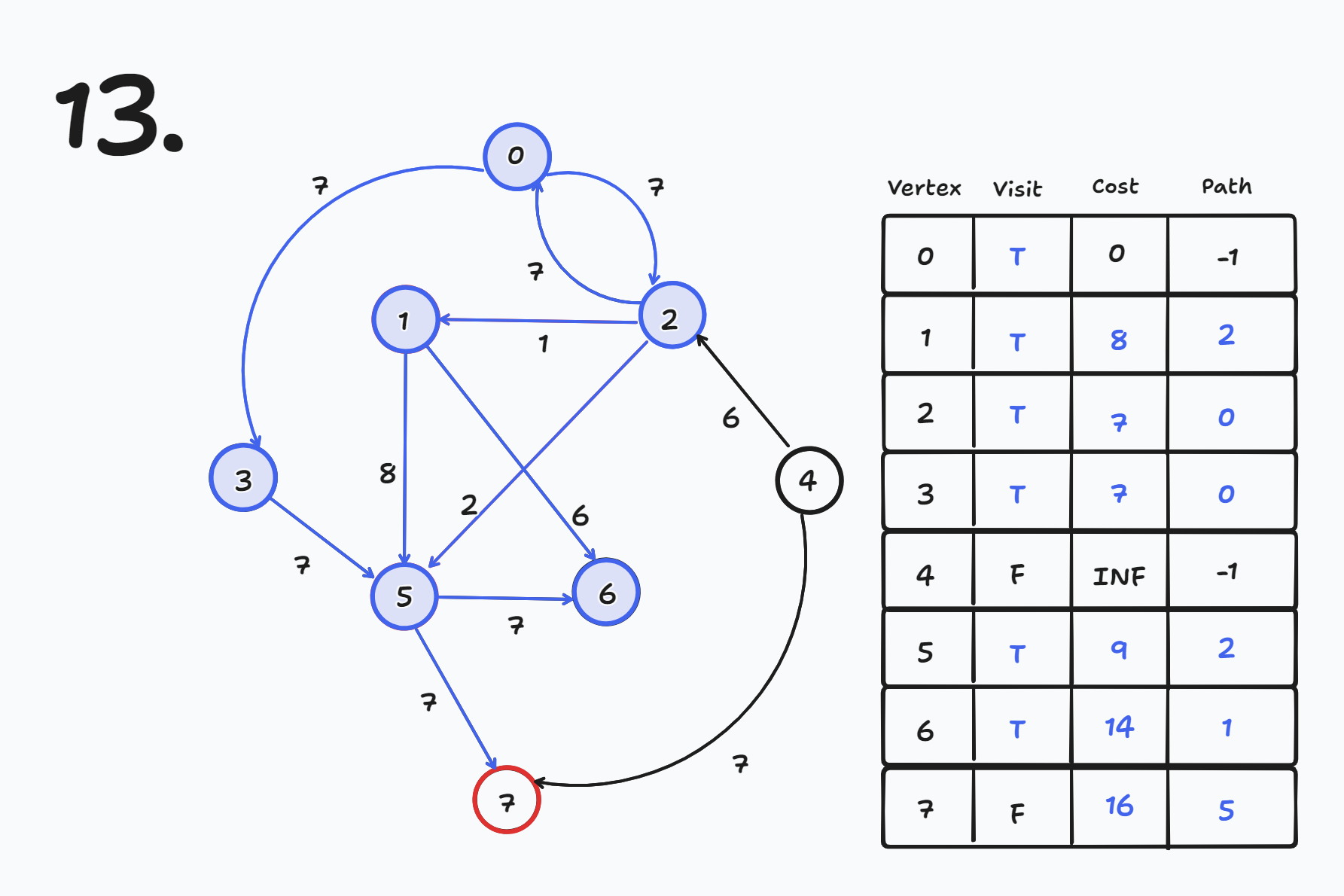
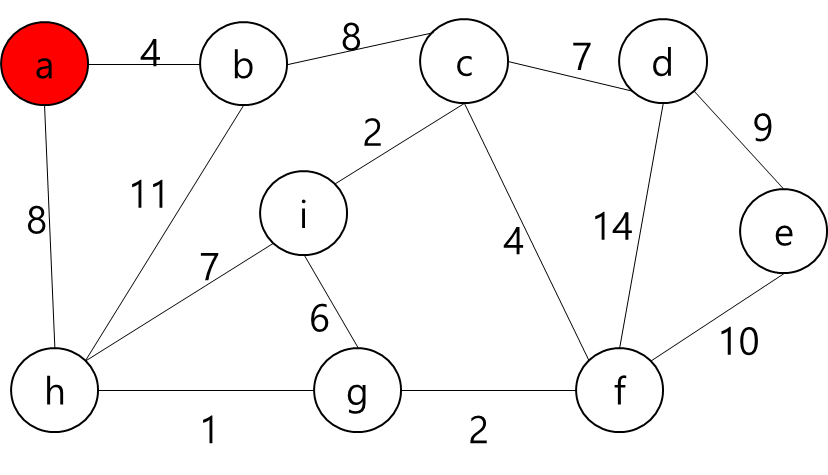
다음과 같은 순서로 간선이 그려졌다고 가정하자 (간선 순서에 따라 갱신 과정이 조금 다를 수 있다)

출발 노드를 0번 노드로 설정한다

• cost[0] = 0

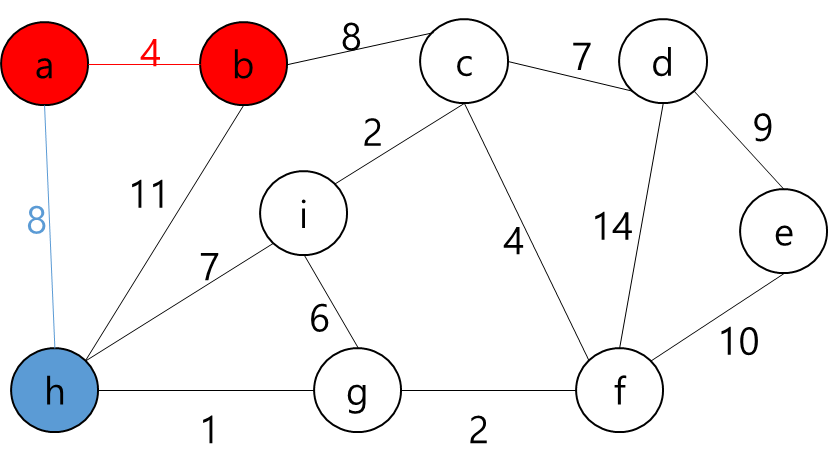
간선 순서에 따라 Relax 연산을 수행하면

1. cost[3] = INF에서 cost[0] + 7 = 7 →  7로 갱신 된다.
   • cost[3] = 7
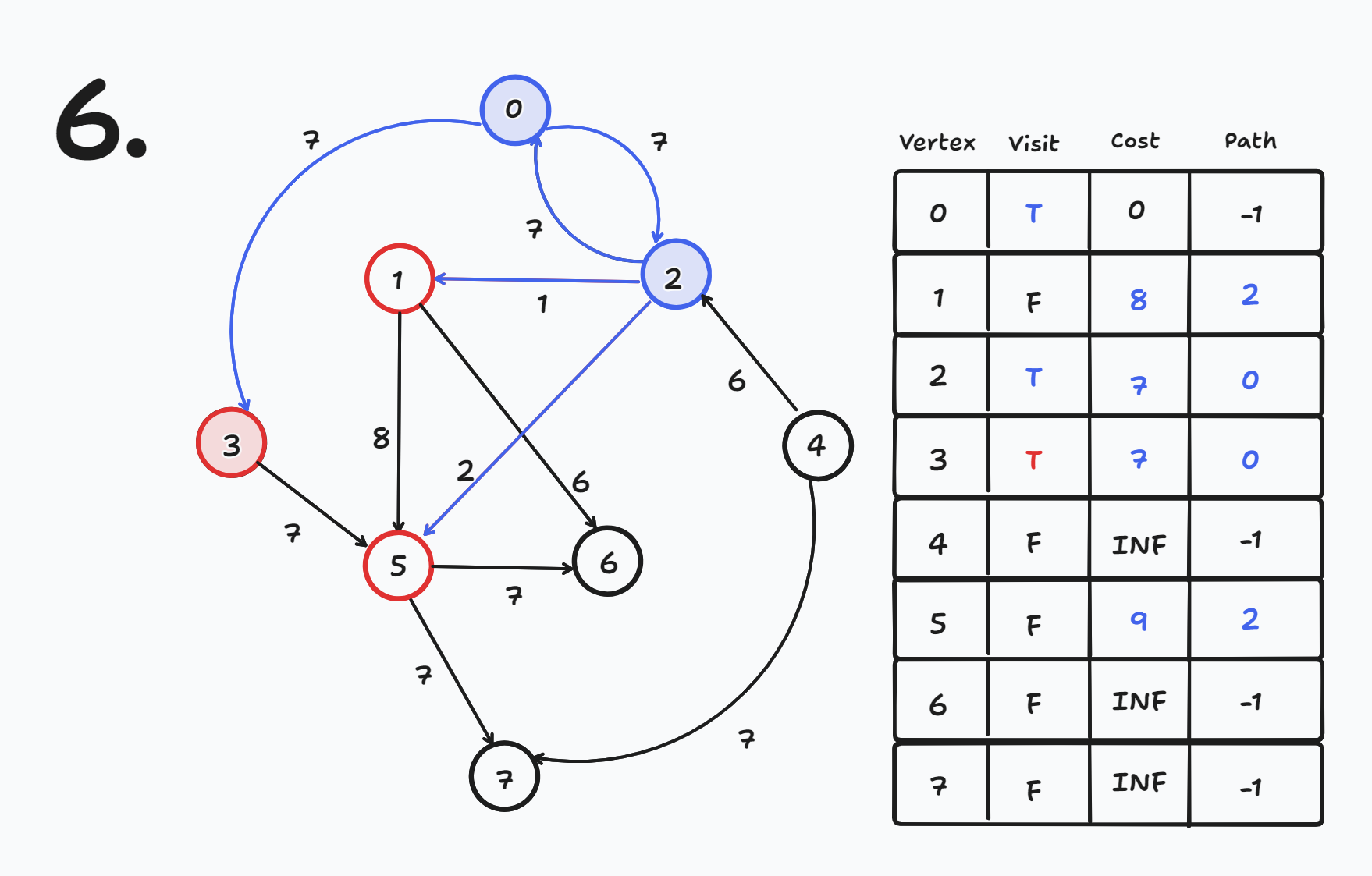
2. cost[2] = INF에서 cost[0] + 7 = 7  → 7로 갱신 된다.
   • cost[2] = 7
3. cost[0] = 0인데 cost[2] + 7 = 14이므로 갱신 되지 않는다.
4. cost[1] = INF인데 cost[2] + 1 = 8 → 8로 갱신 된다.
   • cost[1] = 8
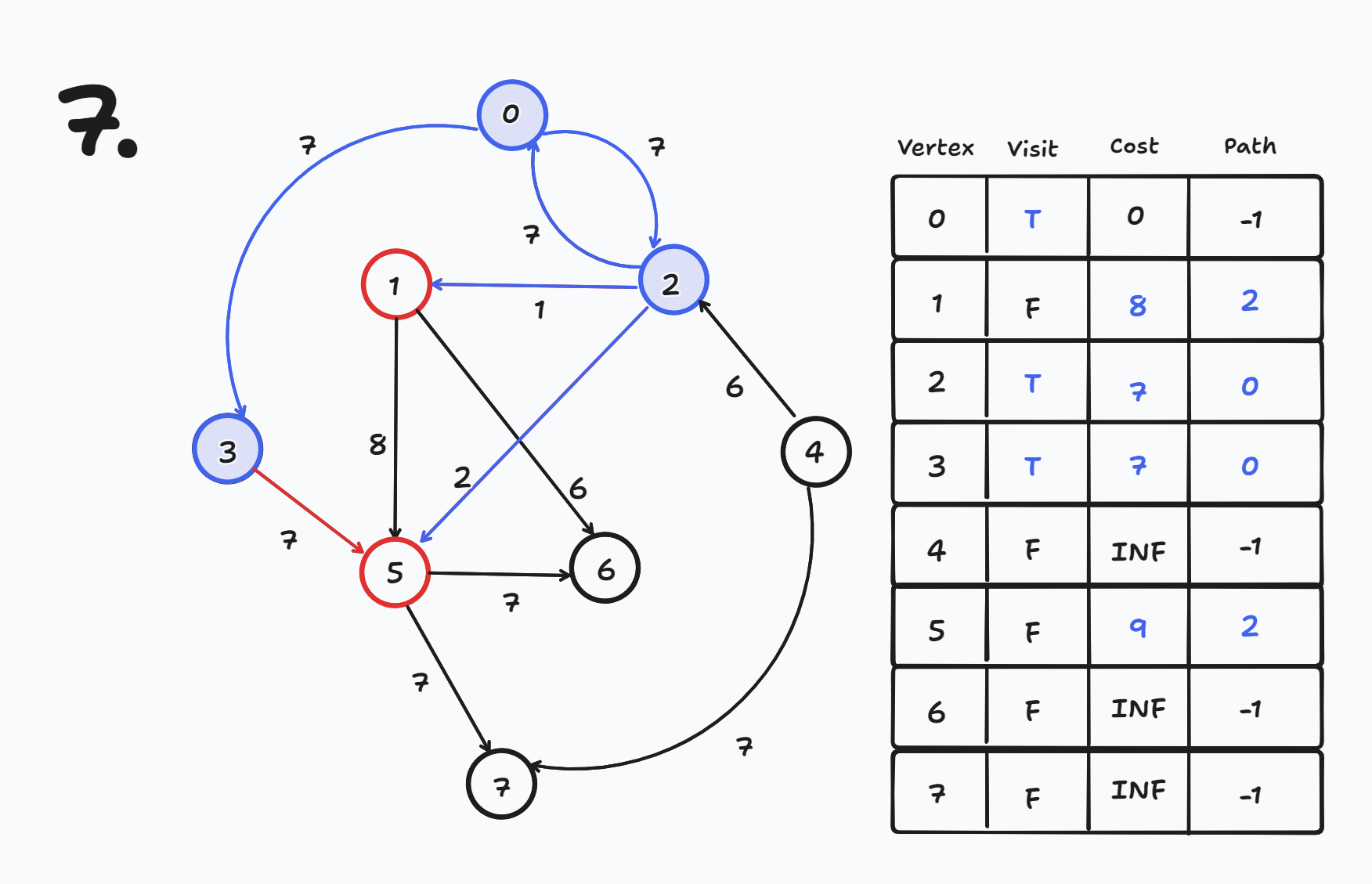
5. cost[5] = INF인데 cost[2] + 2 = 9 → 9로 갱신 된다.
   • cost[5] = 9
6. cost[5] = 9인데 cost[1] + 8 = 16이므로 갱신 되지 않는다.
7. cost[6] = INF인데 cost[1] + 6 = 14 → 14로 갱신 된다.
   • cost[6] = 14
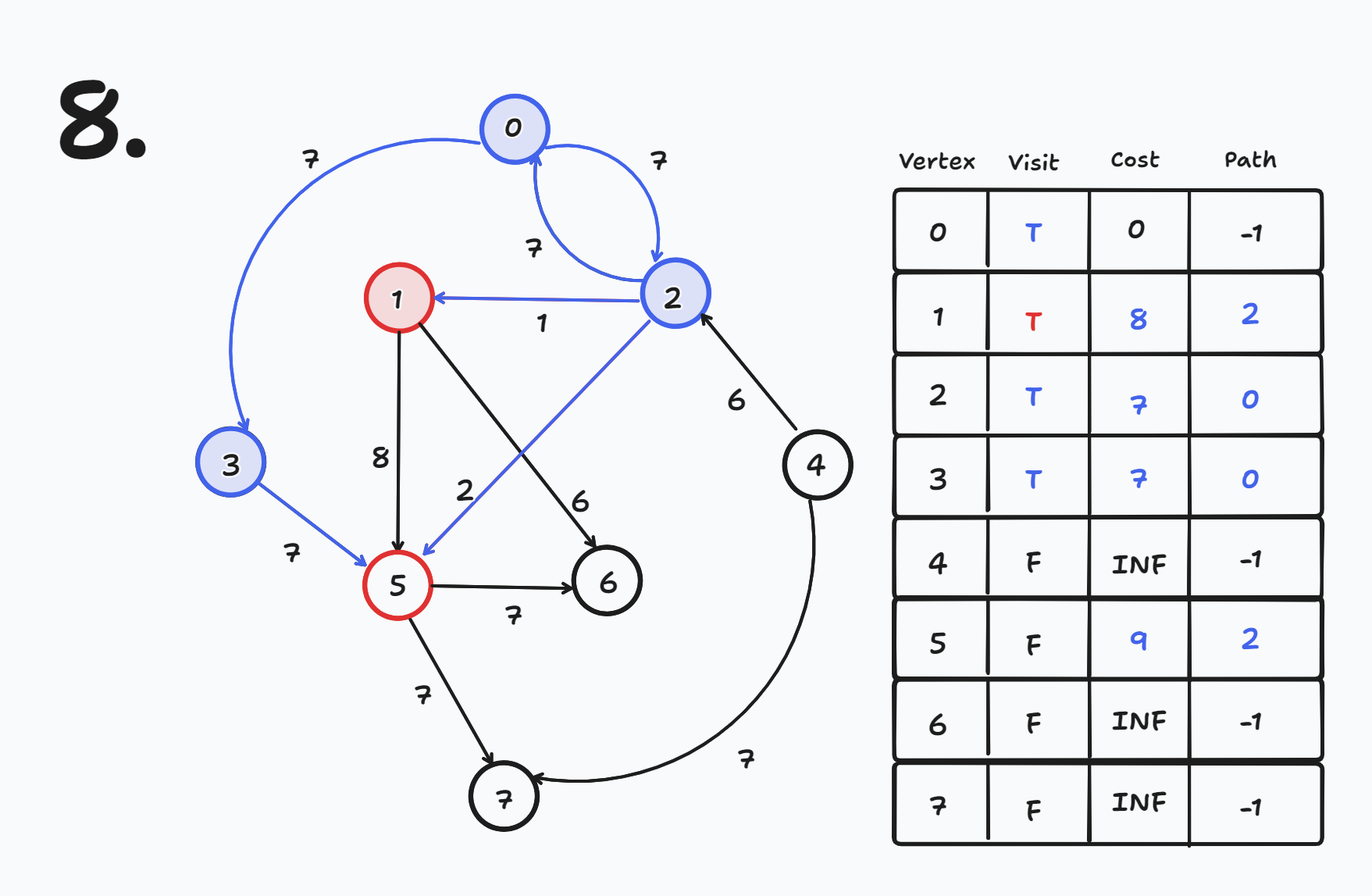
8. cost[5] = 9 인데 cost[3] + 7 = 14이므로 갱신 되지 않는다.
9. cost[6] = 14인데 cost[5] + 7 = 16이므로 갱신 되지 않는다.
10. cost[2] = 7인데 cost[4] + 6 = INF이므로 갱신 되지 않는다.
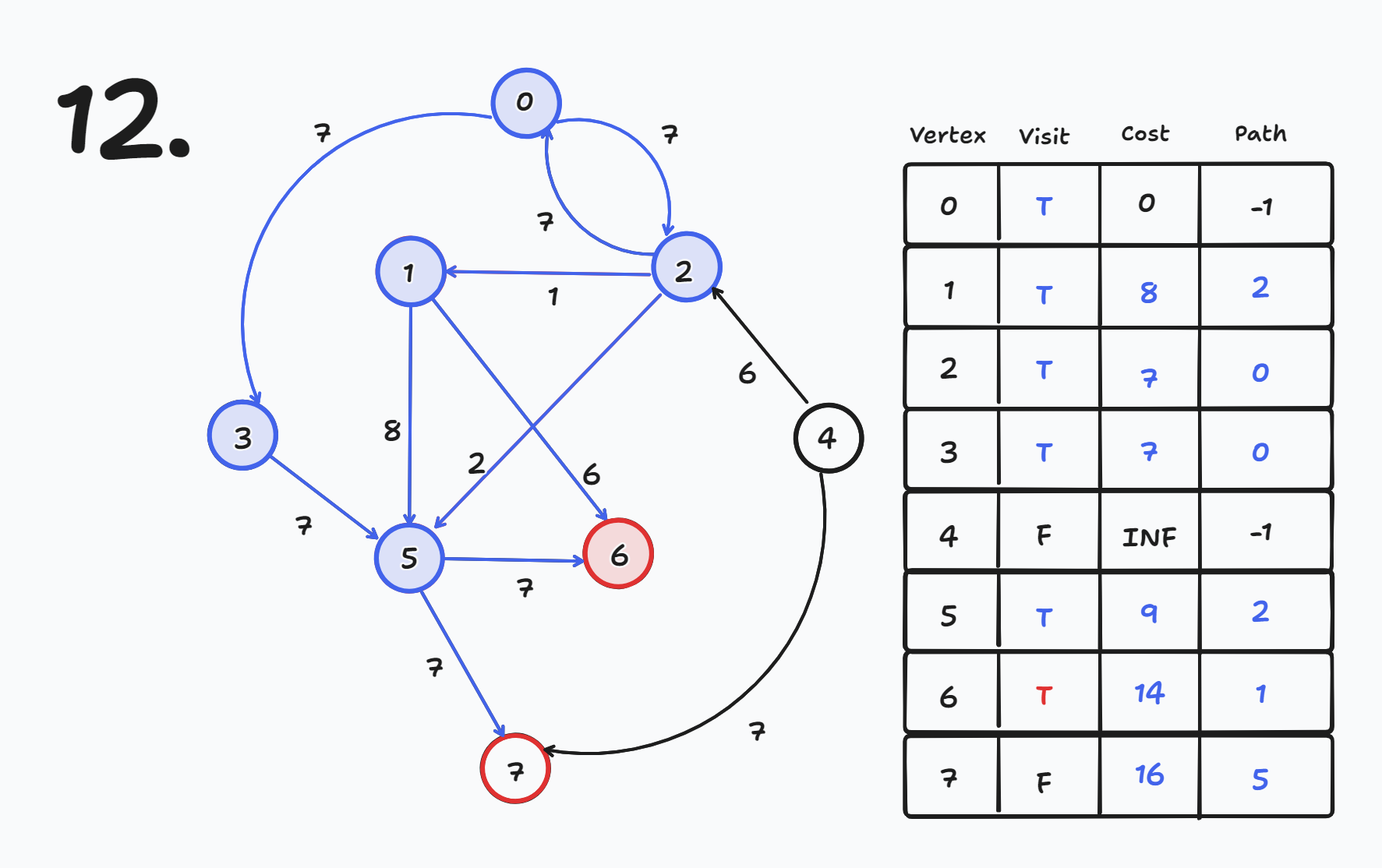
11. cost[7] = INF인데 cost[5] + 7 = 16 → 16으로 갱신 된다.
    • cost[7] = 16
12. cost[7] = INF인데 cost[4] + 7 = INF이므로 갱신 되지 않는다.

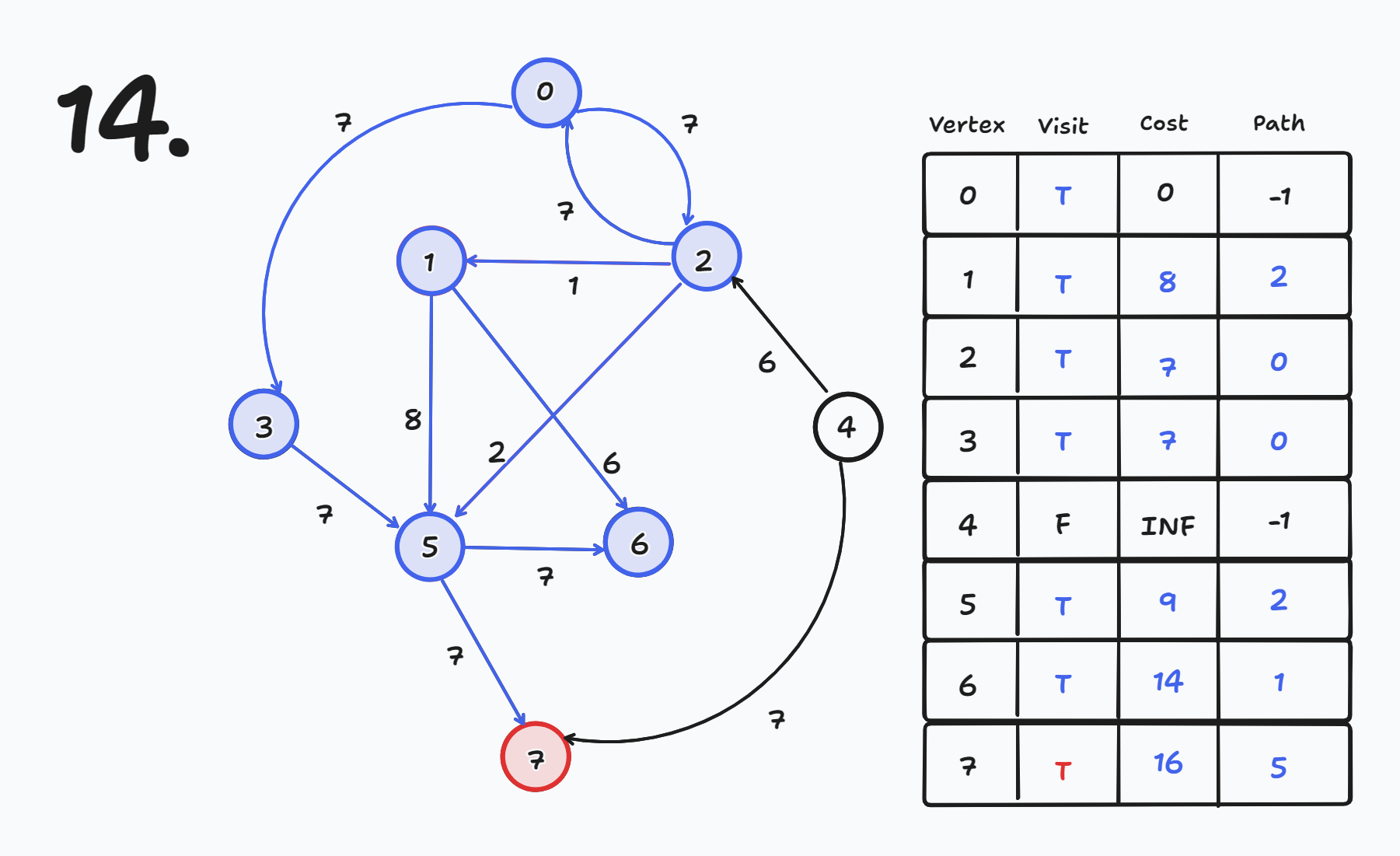
1 Round만에 모두 갱신되어 완성이 되었지만 실제로는 총 N-1번 Round를 한다.

Round가 끝나고 음수 사이클 여부를 확인하기 위해 한번의 Round를 더 수행한다.

• 그 때 다시 갱신이 된다면 음수 사이클이 존재한다는 뜻이다.

# 코드

의사코드

Bellman_Ford(G, w, S) {
	Init(G, S)
    for i = 1 to N-1
    	for each edge(u,v)
        	relax(u,v,w)
    for each edge(u,v)
    	if (cost[v] > cost[u] + w(u,v))
        	then negative-cycle
}

자바 코드

private static int[] bellmanFord() {
    int[] distance = new int[vertexCount + 1];
    Arrays.fill(distance, Integer.MAX_VALUE);
    distance[source] = 0;
    
    for (int i = 0; i < edgeCount; i++) {
    	for (Edge edge : edges) {
            if (distance[edge.from] == Integer.MAX_VALUE) {
            	continue;
            }
            if (distance[edge.to] > distance[edge.from] + edge.weight) {
            	distance[edge.to] = distance[edge.from] + edge.weight;
            }
        }
    }

    for (Edge edge : edges) {
    	if (distance[edge.from] == Integer.MAX_VALUE) {
    		continue;
        }
        if (distance[edge.to] > distance[edge.from] + edge.weight) {
        	return null;
        }
    }

    return distance;
}

# Reference

권오흠 교수님 알고리즘 유튜브 및 강의자료

Algorithm Visualization

# 개요

다익스트라 알고리즘 정리

용어가 좀 혼용 될 수 있다.

• Ex) 노드 == 정점, 엣지 == 간선

# Dijkstra (다익스트라) 알고리즘

• 음수 가중치가 없는 그래프에서 한 정점에서 다른 모든 정점까지의 최단 경로 및 거리를 구하는 알고리즘
• Bellman Ford 알고리즘과의 차이
  • 음수 가중치가 있다면 동작하지 않는다.
  • O(n^2)로 Bellman Ford 알고리즘 보다 빠르다. (우선 순위 큐를 사용한다면 mlogn, m은 간선 개수)

# 동작 과정

그림으로 설명

노드 0부터 다른 모든 노드 까지의 최단 경로 거리를 구하려고 한다.

초기화, 출발 노드가 0번 노드이므로 cost[0] = 0으로 초기화한다.

출발 노드인 0번 노드 방문

• visit[0] = true

현재 노드에서 나가는 간선들에 대해 목적지 노드의 cost와 path를 갱신한다.

• 현재 노드가 0번 노드이므로 0번 노드에서 나가는 간선들에 대해 목적지 노드의 cost와 path를 갱신한다.
  • cost[2] = 7, path[2] = 0
  • cost[3] = 7, path[3] = 0

방문하지 않은 노드들 중 cost가 가장 작은 노드를 방문한다

• 현재 방문하지 않은 노드들 중 cost가 가장 작은 노드는 2,3번인데 index순서에 따라 2번 노드를 방문한다
  • visit[2] = true

현재 노드에서 나가는 간선들에 대해 목적지 노드의 cost와 path를 갱신한다.

• 현재 노드가 2번이므로 2번 노드에서 나가는 간선에 대해 목적지 노드의 cost와 path를 갱신한다.
  • cost[0] = 0 (0 < cost[2] + 7), path[0] = -1 (갱신 X)
  • cost[1] = 8 (INF > cost[2] + 1), path[1] = 2 (갱신 O)
  • cost[5] = 9 (INF > cost[2] + 2), path[5] = 2 (갱신 O)

방문하지 않은 노드들 중 cost가 가장 작은 노드를 방문한다.

• 현재 방문하지 않은 노드들 중 cost가 가장 작은 노드는 3번이므로 3번 노드를 방문한다.
  • visit[3] = true

현재 노드에서 나가는 간선들에 대해 목적지 노드의 cost와 path를 갱신한다.

• 현재 노드가 3번이므로 3번 노드에서 나가는 간선에 대해 목적지 노드의 cost와 path를 갱신한다.
  • cost[5] = 9 (9 < cost[3] + 7), path[5]=2 (갱신 X)

방문하지 않은 노드들 중 cost가 가장 작은 노드를 방문한다.

• 현재 방문하지 않은 노드들 중 cost가 가장 작은 노드는 1번이므로 1번 노드를 방문한다.
  • visit[1] = true

현재 노드에서 나가는 간선들에 대해 목적지 노드의 cost와 path를 갱신한다.

• 현재 노드가 1번이므로 1번 노드에서 나가는 간선에 대해 목적지 노드의 cost와 path를 갱신한다.
  • cost[5] = 9 (9 < cost[1] + 8), path[5] = 2 (갱신 X)
  • cost[6] = 14 (INF > cost[1] + 6), path[6] = 1 (갱신 O)

방문하지 않은 노드들 중 cost가 가장 작은 노드를 방문한다.

• 현재 방문하지 않은 노드들 중 cost가 가장 작은 노드는 5번이므로 5번 노드를 방문한다.
  • visit[5] = true

현재 노드에서 나가는 간선들에 대해 목적지 노드의 cost와 path를 갱신한다.

• 현재 노드가 5번이므로 5번 노드에서 나가는 간선에 대해 목적지 노드의 cost와 path를 갱신한다.
  • cost[6] = 14 (14 < cost[5] + 7), path[6] = 1 (갱신 X)
  • cost[7] = 16 (INF < cost[5] + 7), path[7] = 5 (갱신 O)

방문하지 않은 노드들 중 cost가 가장 작은 노드를 방문한다.

• 현재 방문하지 않은 노드들 중 cost가 가장 작은 노드는 6번이므로 6번 노드를 방문한다.
  • visit[6] = true

현재 노드에서 나가는 간선들에 대해 목적지 노드의 cost와 path를 갱신한다.

• 현재 노드가 6번이므로 6번 노드에서 나가는 간선에 대해 목적지 노드의 cost와 path를 갱신한다.
  • 6번 노드에서 나가는 간선이 없기 때문에 그냥 종료

방문하지 않은 노드들 중 cost가 가장 작은 노드를 방문한다.

• 현재 방문하지 않은 노드들 중 cost가 가장 작은 노드는 7번이므로 7번 노드를 방문한다.
  • visit[7] = true

현재 노드에서 나가는 간선들에 대해 목적지 노드의 cost와 path를 갱신한다.

• 현재 노드가 7번이므로 7번 노드에서 나가는 간선에 대해 목적지 노드의 cost와 path를 갱신한다.
  • 7번 노드에서 나가는 간선이 없기 때문에 그냥 종료

방문하지 않은 노드들 중 cost가 가장 작은 노드를 방문한다.

• 현재 방문하지 않은 노드는 4번 뿐인데, 출발 노드인 0번 노드에서 4번 노드로 가는 경로가 없기 때문에 그냥 종료한다.

종료, 출발 노드인 0번 노드로부터 각 노드의 최단 경로와 그 길이이다.

# 코드 (Java)

의사 코드

// 우선순위 큐 없이

Dijkstra(G, w, S) {
	Init(G, S)
    visit = {}
    cost[S] = 0
    for ( i = 0; i<N; i++) {
    	u = find_minimum_node_not_visit()
        visit[u] = true
        for each v of adjacent u {
        	if cost[v] > cost[u] + w(u,v)
            	then cost[v] = cost[u] + w(u,v)
                and  path[v] = u
        }
    }
}

// 우선순위 큐 사용
Dijkstra(G, w, S) {
	Init(G, S)
    visit = {}
    cost[S] = 0
    pq.add(S, cost[S])
    
    while(pq is not empty) {
    	u = extract_min(pq)
        visit[u] = true
        for each v of adjacent u {
        	if cost[v] > cost[u] + w(u,v)
            	then cost[v] = cost[u] + w(u,v)
                and  path[v] = u
        }
    }
}

시간복잡도

우선순위 큐 없을 시: O(n^2)

우선순위 큐 사용 시: (mlogn^2)

n: 노드 개수, m: 간선 개수

코드 (Java, 우선순위 큐 사용)

public class Dijkstra {	
    static int[] minDistanceFromSource;
    static int[] predecessor;
   	static int vertexCount;
	static int edgeCount;
	static int source;
	static List<Edge>[] graph;
	
    public static void main(String[] args) throws IOException {
		// initGraph() -> 이 부분은 상황에 따라 달라지므로 단순히 이렇게 표현
		dijkstra();    
	}

	private static int[] dijkstra() {
		PriorityQueue<Edge> queue = new PriorityQueue<>(Comparator.comparing(x -> x.weight));
		minDistanceFromSource = new int[vertexCount + 1];
        	predecessor = new int[vertexCount + 1];
       		boolean[] visit = new boolean[vertexCount + 1];
		for (int i = 1; i <= vertexCount; i++) {
			distance[i] = Integer.MAX_VALUE;
		}
		distance[source] = 0;
		queue.add(new Edge(source, source, 0));

		while (!queue.isEmpty()) {
			Edge minEdge = queue.remove();
            	visit[Edge.to] = true;

			for (Edge adjEdge : graph[minEdge.to]) {
				if (distance[adjEdge.to] > distance[adjEdge.from] + adjEdge.weight) {
					distance[adjEdge.to] = distance[adjEdge.from] + adjEdge.weight;
					queue.add(new Edge(adjEdge.from, adjEdge.to, distance[adjEdge.to]));
                    	predecessor[adjEdge.to] = adjEdge.from;
				}
			}
		}
		return distance;
	}
}

class Edge {
	int from;
    int to;
    int weight
    
    public Edge(int from, int to, int weight) {
    	this.from = from;
        this.to = to;
        this.weight = weight;
    }
}

# Reference

권오흠 교수님 유튜브 및 강의자료

알고리즘 Visualization

# 개요

최단 경로 문제 정리

단어가 좀 혼용될 수 있다

• Ex) 노드==정점 / 간선==엣지 

# 최단 경로 문제

가중치가 있는 방향/무방향 그래프에서 두 노드 사이의 가장 짧은 경로를 찾는 문제

# 최단 경로 문제의 유형

Single-Source / Single-Destination (One - to - All)

• 하나의 출발 노드로부터 다른 모든 노드까지의 최단 경로를 찾는 문제
• 모든 노드로부터 하나의 목적지 노드까지의 최단 경로를 찾는 문제
• 방향을 뒤집으면 서로 같아지기 때문에 사실상 같은 유형으로 본다.
• Dijkstra 알고리즘, Bellman Ford 알고리즘

All-Pairs (All - to - All)

• 모든 노드 쌍에 대하여 최단 경로를 찾는 문제
• Floyd-Warshall 알고리즘

# 최단경로와 음수 가중치

Dijkstra 알고리즘은 음수 가중치가 있을 경우 작동하지 않는다.

Bellman-Ford와 Floyd-Warshall 알고리즘은 음수 사이클이 없다는 가정하에 음수 가중치가 있어도 작동한다.

음수 사이클

음수 사이클이 있으면 최단 경로가 정의되지 않는다.

• 사이클의 합이 음수라면 계속 사이클을 돌게 되고 결국 합이 -∞되어 최단 경로를 찾을 수 없다.
• 단, 그래프 내에 음수 사이클이 있어도 그 사이클이 목적지까지 가는 경로에 없다면 상관없다.

# 최단 경로 문제의 기본 특성

1. 최단 경로의 어떤 부분 경로 역시 최단 경로이다. (Optimal SubStructure → DP)

• 위 경로가 u → v의 최단 경로라면, x → y의 경로 또한 최단 경로이다.

증명 (귀류법)

• 만약 더 짧은 경로(x → y)가 있다고 가정해보자
• 이 경로가 더 짧다면 u → v의 최단 경로는 u → v가 아니라 x → y를 거쳐가는 u → x → y → v가 될 것이다.
• 이것은 처음 가정(u →v 가 최단 경로라면)의 모순이 된다.
• 그러므로 최단 경로의 부분 경로도 최단 경로이다.

2.  최단 경로는 사이클을 포함하지 않는다.

# Single-Source 최단 경로 문제

음수 사이클이 없는 가중치 방향 그래프 G = (V, E)와 출발 노드 S에서 각 노드 v에 대하여 다음을 계산한다.

• d[v] (distance estimation): 출발 노드 S로부터 각 노드v에 대하여 현재까지 알고 있는 최단 경로의 길이 (→ 알고리즘이 진행됨에 따라 갱신 된다.)
  
  • 처음에는 d[S] = 0, 각 d[v]들은 ∞으로 초기화한다.
    • S는 출발 노드이고, 음수 사이클이 없으므로 가장 작은 값인 0
    • 그 외의 다른 노드들 v는 아직 탐색 시작을 안했으므로 ∞
  • 알고리즘이 수행됨에 따라 d[v]가 점점 감소하며 최종적으로 d[v]값이 S →  v의 최단 경로 길이가 된다.
• π[v] (predecessor): S에서 v까지의 최단 경로 상에서 v의 직전 노드
  • 처음에는 π[v]와 π[S]는 null로 초기화
    • 출발 노드S의 이전 노드는 없으므로 null
    • 다른 노드들 v는 아직 탐색 시작을 안했으므로 null
  • 최단경로의 길이 외에 그 경로 자체를 요구할 수 있으므로 이전 노드를 기록하며 역추적한다.

기본 연산: Relaxation

1. d[u] = 5, d[v] = 9, w(u,v) = 2(간선 u → v의 가중치 값)인 상황

• d[v]는 "현재까지 알고 있는" S → v의 최단 경로 길이 이므로 Relaxation 연산에  따라 갱신 될 수 있다.
• 기존에 알고 있는 S →  v의 최단 경로는 S →  v로 d[v] = 9 였는데 더 짧은 경로인 S → u → v경로를 발견했으므로 d[v] = d[u] + w(u,v)로 갱신한다 (9 > 5+2)

2. d[u] = 5, d[v] = 6, w(u,v) = 2인 상황

• Relaxation 연산을 했지만 기존 최단 경로인 S → v d[v]가 더 짧은 경로이므로 갱신하지 않는다.

Relaxtaion 의사 코드

Relax(u, v, w) {
	if(d[v] > d[u] + w(u,v))
    	then d[v] ← d[u] + w(u,v)
        	 π[v] ← u
}

대부분의 Single-Source 최단 경로 알고리즘의 기본 구조

1. 초기화: d[S] = 0, 노드 v에 대해 d[v] = ∞, π[v]=null
2. 간선들에 대해서 반복적인 Relaxtation 연산

의사 코드

Generic-Single-Source(G, w, S) {
	Init(G, S)
    Repeat
    	for each edge(u,v)
        	Relax(u,v,w)
    until there is no change
}

1. 의문: 이렇게 반복하면 최단 경로가 정말 찾아질까?
2. 의문: 찾아진다면 몇 번 반복해야 찾아질까?

증명

• 가정: N개의 정점에서, S → vn 경로가 최단 경로라면 이 경로에 포함된 간선의 개수는 최대 N-1개이다.
• 첫 번째 Round
  • 모든 간선들에 대해 Relax연산을 하고, d[S] = 0, d[v1]이  ∞에서 d[S] + w(S, v1)을 통해 갱신 된다.
  • S → vn까지의 최단 경로의 부분 경로 역시 최단 경로이므로 갱신 된 d[v1]이 곧 최단 경로가 된다.
• 두 번째 Round
  • 모든 간선들에 대해 Relax연산을 하고, d[v2]이  ∞에서 d[v1] + w(v1, v2)을 통해 갱신 된다.
  • 마찬가지로 갱신 된 d[v1]이 곧 최단 경로가 된다.
• 반복하면 d[vn]은 n-1번째 Round에 최단 경로가 된다.
• 즉 노드의 개수가 N개라면 N-1번의 반복으로 모든 노드의 최단 경로를 구할 수 있다.

직관적으로 봐도 vn까지 최단 경로의 간선 수는 최대 N-1라는 것을 생각할 수 있는데

• vx를 거쳐가는 더 짧은 경로가 있다면? → 그럼 그 경로가 최단 경로가 되며, N개의 정점에서 N+1개의 정점이 되었다. 그러므로 간선의 개수는 최대 N개가 될 것이다.

• v2 → v3 → v4 경로를 통해 가는 것보다 v3 → v2 갔다가 다시 v2 → v3으로 가는 것이 더 빠르다면? → 그 자체로 음수 사이클이 생긴다는 뜻이며 음수 사이클이 없다는 전제에 모순된다.

Worst Case

시간 복잡도: O(n^3) → 효율적인 알고리즘이라고 할 수 없다.

다음과 같은 상황을 보자

• 첫 번째 Round에서 간선들을 어떠한 순서로 Relax 연산을 하다보니 d[v] = 1000이 되었다.
• 두 번째 Round에서 간선들을 어떠한 순서로 Relax 연산을 하다보니 d[v] = 800이 되었다.
• 최악의 상황은 마지막 Round에서 d[v] = 200으로 갱신 되고 이것이 최단 경로라는 것을 알게 되었을 때이다. 그제서야 v 이후의 노드들에 대한 최단 경로를 알 수 있게 된다.
• 하지만 처음부터 가중치가 50인 경로로 Relax를 했다면 더 빠르게 최단 경로를 찾을 수 있지 않았을까?
  • Dijkstra 알고리즘으로 해결
• 최악의 경우 시간 복잡도가 O(n^3)인데도 사용하는 이유는 가중치가 음수일 때도 동작하고, 음수 사이클 여부를 알 수 있기 때문이다.

# Reference

권오흠 교수님 유튜브 및 강의자료

Prim(프림) 알고리즘

그래프의 모든 정점을 최소 비용으로 연결하는, 즉, 최소 신장 트리를 구현하는 대표적인 Greedy(탐욕) 알고리즘이다.

Greedy 알고리즘

• 그 순간에 가장 좋다고 생각되는 해를 선택
  • MST에 포함된 정점들과 그렇지 않은 정점들을 잇는 간선중 가장 가중치가 작은 간선을 선택하여 MST에 추가
• 그 순간에는 최적의 해일 수 있지만, 전체적으로 봤을때는 그렇지 않을 수 있으므로 반드시 검증을 해야함
  • 정점이 이미 선택되어 MST에 포함되어 있는지 검증
• Kruskal(크루스칼) 알고리즘의 경우는 간선을 선택하는 Greedy 알고리즘이다.

동작방식

1. 임의의 정점을 출발 정점으로 선택
2. 매 단계에서 이전단계에 MST에 포함된 정점들과 포함되지 않은 정점들을 잇는 간선 중 가중치가 가장 작은 간선을 선택하여 MST를 확장한다.
3. 간선개수가 \(N-1\)이 될 때까지 반복(\(N\): 정잠개수)

Visualize

임의의 정점 a를 선택한다.

MST에 포함된 정점들(a)과 그렇지 않은 정점들을 잇는 간선들 중에 가중치가 가장 작은 간선 (a,b)를 MST에 추가 

MST에 포함된 정점들(a,b)과 그렇지 않은 정점들을 잇는 간선 중 가중치가 가장 작은 간선((a,h))를 MST에 추가

MST에 포함된 정점들(a,b,h)과 그렇지 않은 정점들을 잇는 간선 중 가중치가 가장 작은 간선((h,g))를 MST에 추가

MST에 포함된 정점들(a,b,h,g)과 그렇지 않은 정점들을 잇는 간선 중 가중치가 가장 작은 간선((g,f))를 MST에 추가

MST에 포함된 정점들(a,b,h,g,f)과 그렇지 않은 정점들을 잇는 간선 중 가중치가 가장 작은 간선((c,f))를 MST에 추가

MST에 포함된 정점들(a,b,h,g,f,c)과 그렇지 않은 정점들을 잇는 간선 중 가중치가 가장 작은 간선((c,i))를 MST에 추가

MST에 포함된 정점들(a,b,h,g,f,c,i)과 그렇지 않은 정점들을 잇는 간선 중 가중치가 가장 작은 간선((d,e))를 MST에 추가

모든 정점들이 MST에 포함되어 있고 간선의 개수가 정점 개수 - 1 이므로 끝

시간 복잡도

간선의 가중치가 최소인 간선 탐색: \(O(n)\)

MST에 포함된 정점과 그렇지 않은 정점들 사이의 거리 갱신: \(O(n)\)

이것을 정점의 수 만큼 반복하므로 \((O(n) + O(n)) * (n-1) = O(n^2)\)

그러나 우선순위 큐(Priority Queue)를 사용하는 경우에는 \(O(nlgn)\)이다.

코드

class MSTPrim {
  int[][] graph;
  
  public MSTPrim() {
    this.graph = {
      {0, 4, 0, 0, 0, 0, 0, 8, 0},
      {4, 0, 8, 0, 0, 0, 0, 11, 0},
      {0, 8, 0, 7, 0, 4, 0, 0, 7},
      {0, 0, 7, 0, 9, 14, 0, 0, 0},
      {0, 0, 0, 9, 10, 0, 0, 0, 0},
      {0, 0, 4, 14, 10, 0, 2, 0, 0},
      {0, 0, 0, 0, 0, 2, 0, 1, 7},
      {8, 11, 0, 0, 0, 0, 1, 0, 7},
      {0, 0, 2, 0, 0, 0, 6, 7, 0},
    };
  }
  
  public int prim(startVertex) {
    int vertexCount = graph.length;
    int[] distance = new int[vertexCount];
    boolean[] visit = new boolean[vertexCount];
    Arrays.fill(distance, Integer.MAX_VALUE);
    
    int result = 0;
    distance[startVertex] = 0;
    
    for(int i = 0; i < vertexCount; i++) {
      int minDistanceFromMst = Integer.MAX_VALUE;
      int targetVertex = -1;
      for(int j = 0; j < vertexCount; j++) {
        if(!visit[j] && distance[j] < minDistanceFromMst) {
          minDistanceFromMst = distance[j];
          targetVertex = j;
        }
      }
      
      visit[targetVertex] = true;
      result += minDistanceFromMst;
      
      for(int j = 0; j < vertexCount; j++) {
        if(!visit[j] && graph[targetVertex][j] > 0 && graph[targetVertex][j] < distance[j]) {
          distance[j] = graph[targetVertex][j];
        }
      }
    }
    
    return result; 
  }
  
  public int prim_using_priority_queue(startVertex) {
    int vertexCount = graph.length;
    boolean[] visit = new boolean[vertexCount];
    // int[] -> {destination, weight}
    PriorityQueue<int[]> queue = new PriorityQueue<>(Comparator.comparingInt(x -> x[1]);
    
    queue.add(new int[]{startVertex, 0})
    int result = 0;
    
    while(!queue.isEmpty()) {
      int[] current = queue.poll();
      int destination = current[0];
      int weight = current[1];
      if(visit[destination]) {
        continue;
      }
      
      visit[destination] = true;
      result += weight;
      
      for(int i = 0; i < vertexCount; i++) {
        if(!visit[i] && graph[destination][i] > 0) {
          queue.add(new int[]{i, graph[destination][i]};
        }
      }
    }
    
    return result; 
  }
}

같이 볼 자료

2022.01.16 - [Algorithm] - [Algorithm] MST (Minimum Spanning Tree, 최소 신장 트리)

2022.01.16 - [Algorithm] - [Algorithm] Krsukal (크루스칼) 알고리즘

Kruskal (크루스칼) 알고리즘

그래프의 모든 정점을 최소 비용으로 연결하는, 즉, 최소 신장 트리를 구현하는 대표적인 Greedy(탐욕) 알고리즘이다.

Greedy 알고리즘

• 그 순간에 가장 좋다고 생각되는 해를 선택
  • 정렬 된 간선 중 가중치가 가장 작은 간선부터 차례대로 선택
• 그 순간에는 최적의 해일 수 있지만, 전체적으로 봤을때는 그렇지 않을 수 있으므로 반드시 검증을 해야함
  • 이미 선택된 간선인지, 사이클을 형성하는지 검증
• Prim(프림) 알고리즘의 경우는 정점을 선택하는 Greedy 알고리즘이다.

동작방식

1. 그래프의 간선들을 오름차순으로 정렬한다.
2. 정렬된 간선들을 차례대로 선택한다.
3. 단, 이미 선택된 간선과 사이클을 형성하는 간선은 패스
4. 간선의 개수가 \(N-1\)개가 될 때까지 반복한다 (\(N\): 정점 개수)

Visualize

처음은 어떠한 정점들도 선택되지 않은 상태, 간선들을 오름차순 정렬

정렬된 간선을 차례대로 선택하여 MST에 추가한다. 간선 (g,h)를 추가하고 정점 g,h를 같은 집합으로 합친다.

간선 (c,i)를 추가하고 정점 c와 i를 같은 집합으로 합친다.

간선 (g,f)를 추가하고 정점 f와 g를 같은 집합으로 합친다.

간선 (a,b)를 추가하고 정점 a와 b를 같은 집합으로 합친다.

간선 (c,f)를 추가하고 정점 c와 f를 같은 집합으로 합친다.

간선 (g,i)를 추가하려고 하는데.. 정점 g와 i는 이미 같은 집합이다. 만약 간선 (g,i)를 추가하면 사이클이 형성된다. 그러므로 그냥 패스

간선 (c,d)를 추가하고 정점 c와 d를 같은 집합으로 합친다.

간선 (h,i)를 추가하려고 하는데.. 정점 h와 i는 이미 같은 집합이다. 만약 간선 (h,i)를 추가하면 사이클이 형성된다. 그러므로 그냥 패스

간선 (a,h)를 추가하고 a와 h를 같은 집합으로 합친다.

간선 (b,c)를 추가하려고 하는데... b와 c는 이미 같은 집합이다. 만약 간선 (b,c)를 추가한다면 사이클이 형성된다. 그러므로 그냥 패스

간선 (d,e)를 추가하고 정점 d와 e를 같은 집합으로 합친다.

모든 정점들이 같은 집합이고, MST에 추가된 간선이 정점 개수 - 1이므로 끝

사이클을 형성하는 지 검증할 때 Union-Find 알고리즘을 사용한다

시간복잡도

Union-Find 알고리즘을 사용하면 간선들을 정렬하는 시간에 영향받는다.

즉, 간선 \(E\)개를 Quick Sort의 효율로 정렬한다면 \(O(ElogE)\)이다.

코드

class MSTKruskal {
  int[] parents;
  int[][] graph;
  
  public MSTKruskal() {
    this.graph = {
      {0, 4, 0, 0, 0, 0, 0, 8, 0},
      {4, 0, 8, 0, 0, 0, 0, 11, 0},
      {0, 8, 0, 7, 0, 4, 0, 0, 7},
      {0, 0, 7, 0, 9, 14, 0, 0, 0},
      {0, 0, 0, 9, 10, 0, 0, 0, 0},
      {0, 0, 4, 14, 10, 0, 2, 0, 0},
      {0, 0, 0, 0, 0, 2, 0, 1, 7},
      {8, 11, 0, 0, 0, 0, 1, 0, 7},
      {0, 0, 2, 0, 0, 0, 6, 7, 0},
    }
  }
  
  public int kruskal() {
    int[][] edges = buildEdges();
    makeSet();
    int result = 0;
    
    for(int i = 0; i < edges.lengh; i++) {
      int source = edges[i][0];
      int destination = edges[i][1];
      int weight = edges[i][2];
      
      if(find(source) != find(destination)) {
        union(source, destination);
        result += weight;
      }
    }
    
    return result;
  }
  
  public int[][] buildEdges() {
    int[][] edges = new int[][]{};
    index = 0;
    
    for(int i = 0; i < graph.length; i++) {
      for(int j = 0; j < graph.length; j++) {
        if(graph[i][j] !=0) {
          edges[index++] = {i, j, graph[i][j]};
          edges[index++] = {j, i, graph[j][i]};
        }
      }
    }
    
    return edges;
  }
  
  public void makeSet() {
    this.parents = new int[graph.length];
    
    for(int i = 0; i < graph.lenght; i++) {
      parents[i] = i;
    }
  }
  
  public int find(x) {
    if(parents[x] == x) {
      return x;
    }
    
    return parents[x] = find(parents[x]);
  }
  
  public int union(x, y) {
    x = find(x);
    y = find(y);
    
    if(x == y) {
      return;
    }
    
    if(x > y) {
      parents[y] = x;
    } else {
      parents[x] = y;
    }
    
  }
}

같이 볼 자료

2022.01.16 - [Algorithm] - [Algorithm] MST (Minimum Spanning Tree, 최소 신장 트리)

2022.01.16 - [Algorithm] - [Algorithm] Prim(프림) 알고리즘

신장 트리 (Spanning Tree)

• 그래프의 모든 정점을 연결하는 트리
• 트리: 일반적으로 계층구조의 자료구조를 생각하는데, 그래프 이론에서 사이클이 없는 무방향 그래프를 트리라고 한다.
• 그래프가 n개의 정점을 가질 때, 그래프의 최소 간선의 수는 n-1개이다.
• 하나의 그래프에서 여러개의 신장 트리가 존재할 수 있다.

최소 신장 트리 (Minimum Spanning Tree)

• Spanning Tree 중에서 사용된 간선들의 가중치 합이 최소인 트리
• Spanning Tree와 마찬가지로 정점이 N개일 때, N-1개의 간선으로 연결된다.
• Spanning Tree와 마찬가지로 사이클이 없다.
• Spanning Tree와 마찬가지로 MST의 해가 여러개 일 수 있다.

MST을 구현하는 알고리즘으로 Kruskal(크루스칼) 알고리즘과 Prim(프림) 알고리즘이 있다.

2022.01.16 - [Algorithm] - [Algorithm] Krsukal (크루스칼) 알고리즘

2022.01.16 - [Algorithm] - [Algorithm] Prim(프림) 알고리즘

그래프 순회

• 그래프에서 임의의 한 정점에서 출발하여 모든 정점을 한번씩 방문하는 작업
• 탐색하는 동안 이미 방문한 정점이 있을 수 있으므로 방문했다는 표시를 하여 중복방문을 피한다.
• 대표적으로 DFS, BFS가 있다.

BFS (Breath-First-Search): 너비 우선 탐색

• 출발노드에서 인접한 노드(형제노드)를 먼저 탐색하는 방식
• 가중치가 없는 그래프에서 최단경로를 찾을 때 사용한다.
• 일반적으로 Queue를 이용하여 구현한다.

동작방식

1. 시작정점을 방문하여 큐에 삽입한다.
2. 큐에서 정점을 꺼내 정점에서 인접한 정점중, 방문하지 않은 정점들을 방문하여 큐에 삽입한다.
3. 모든 정점을 반복할 때까지 반복한다.

Visualize

E노드에서 더이상 간선이 없으므로 그냥 큐에서 꺼내는것으로 끝이다

G노드에서 더이상 간선이 없으므로 그냥 큐에서 꺼내는것으로 끝이다. H노드와 I노드도 마찬가지이다.

코드

의사코드

BFS(graph, start_node) {
  Queue q;
  boolean[] visit;
  
  q.add(start_node);
  visit[start_node] = true;
  
  while(!q.isEmpty()) {
    current_node = q.pop();
    for(adjacent_node to current_node) {
      if(!visit[adjacent_node]) {
        visit[adjacent_node] = true;
        q.add(adjacent_node);
      }
    }
  }
}

코드 - Queue (Java)

class BFS_Queue {
  private int[][] graph;
  private boolean[] visit;
  
  public BFS_Queue() {
    this.graph = {
      {0, 1, 1, 1, 0, 0, 0, 0, 0},
      {1, 0, 0, 0, 1, 0, 0, 0, 0},
      {1, 0, 0, 0, 0, 1, 1, 0, 0},
      {1, 0, 0, 0, 0, 0, 0, 1, 0},
      {0, 1, 0, 0, 0, 0, 0, 0, 0},
      {0, 0, 1, 0, 0, 0, 0, 0, 1},
      {0, 0, 1, 0, 0, 0, 0, 0, 0},
      {0, 0, 0, 1, 0, 0, 0, 0, 0},
      {0, 0, 0, 0, 0, 1, 0, 0, 0},
    };
    this.visit = new boolean[graph.length];
  }
  
  public void bfs(startNode) {
    Queue<Integer> queue = new LinkedList();
    
    queue.add(startNode);
    visit[startNode] = true;
    
    while(!queue.isEmpty()) {
      int currentNode = queue.poll();
      
      for(int i = 0; i < graph[currentNode].length; i++) {
        if(isAdjacentNode(currentNode, i) && !visit[i]) {
          visit[i] = true;
          queue.add(i);
        }
      }
    }
  }
  
  public boolean isAdjacentNode(int currentNode, int targetNode) {
    return graph[currentNode][targetNode] == 1;
  }
}

시간 복잡도

• 인접 리스트: \(O(N+E)\) (\(N\): 정점 개수, \(E\): 간선 개수)
• 인접 행렬: \(O(N^2)\)

참고

2021.04.14 - [Algorithm] - [Algorithm] 그래프 (Graph)

2022.01.08 - [Algorithm] - [Algorithm] DFS (Depth-First-Search, 깊이 우선 탐색)

그래프 순회

• 그래프에서 임의의 한 정점에서 출발하여 모든 정점을 한번씩 방문하는 작업
• 탐색하는 동안 이미 방문한 정점이 있을 수 있으므로 방문했다는 표시를하여 중복방문을 피한다.
• 대표적으로 DFS와 BFS가 있다.

DFS (Depth-First-Search): 깊이 우선 탐색

• 출발노드에서 하위노드(자식노드)를 먼저 탐색하는 방식
• 일반적으로 Stack이나 Recursive를 이용하여 구현한다.

동작방식

1. 시작노드에서 간선을 따라 다음노드로 방문한다.
2. 더이상 탐색할 간선이 없다면 역추적(Backtracking)을 통해 이전노드로 이동하여 아직 탐색하지 않은 간선을 참색한다.
3. 모든 노드를 탐색할 때까지 반복한다.

Visualize

E노드에서 더이상 이동 할 간선이 없으므로 역추적으로 통해 B노드로 이동, B노드에서도 마찬가지로 더이상 이동할 간선이 없으므로 A노드로 이동 후 다음 간선인 (A,C)을 통해 C노드로 이동

F노드에서 더이상 이동할 간선이 없으므로 역추적을 통해 C노드로 이동, C노드에서 다음 간선인 (C,G)을 통해 G노드로 이동

I노드에서 더이상 이동할 간선이 없으므로 역추적을 통해 G노드로 이동, G노드에서도 마찬가지로 C노드로 이동, C노드에서도 마찬가지로 A노드로 이동, A노드에서 다음 간선인 (A,D)를 통해 D노드로 이동

코드

의사코드

DFS(graph, current_node, visit) {
  visit[current_node] = true
  
  for( adjacent_node to current_node) {
    if(!visit[adjacent_node]) {
      DFS(graph, adjacent_node, visit)
    }
  }
}

코드 - Recursive (Java)

class DFS_Recursive {

  private int[][] graph;
  
  private boolean[] visit;
  
  public DFS_Recursive() {
    this.graph = {
      {0, 1, 1, 1, 0, 0, 0, 0, 0},
      {1, 0, 0, 0, 1, 0, 0, 0, 0},
      {1, 0, 0, 0, 0, 1, 1, 0, 0},
      {1, 0, 0, 0, 0, 0, 0, 1, 0},
      {0, 1, 0, 0, 0, 0, 0, 0, 0},
      {0, 0, 1, 0, 0, 0, 0, 0, 1},
      {0, 0, 1, 0, 0, 0, 0, 0, 0},
      {0, 0, 0, 1, 0, 0, 0, 0, 0},
      {0, 0, 0, 0, 0, 1, 0, 0, 0},
    };
    visit = new boolean[graph.length];
  }
  
  public void dfs(currentNode) {
    visit[currentNode] = true;
    
    for(int i = 0; i < graph[currentNode].length; i++) {
      if(isAdjacentNode(currentNode, i) && !visit[i]) {
        dfs(i);
      }
    }
  }
  
  public boolean isAdjacentNode(int currentNode, int targetNode) {
    return graph[currentNode][targetNode] == 1;
  }

}

코드 - Stack

class DFS_Stack {

  private int[][] graph;
  
  private boolean[] visit;
  
  public DFS_Stack() {
    this.graph = {
      {0, 1, 1, 1, 0, 0, 0, 0, 0},
      {1, 0, 0, 0, 1, 0, 0, 0, 0},
      {1, 0, 0, 0, 0, 1, 1, 0, 0},
      {1, 0, 0, 0, 0, 0, 0, 1, 0},
      {0, 1, 0, 0, 0, 0, 0, 0, 0},
      {0, 0, 1, 0, 0, 0, 0, 0, 1},
      {0, 0, 1, 0, 0, 0, 0, 0, 0},
      {0, 0, 0, 1, 0, 0, 0, 0, 0},
      {0, 0, 0, 0, 0, 1, 0, 0, 0},
    };
    visit = new boolean[graph.length];
  }
  
  public void dfs(startNode) {
    Stack<Integer> stack = new Stack();
    
    stack.push(startNode);
    visit[startNode] = true;
    
    while(!stack.isEmpty()) {
      int currentNode = stack.pop();
      
      for(int i = 0; i < graph[currentNode].length; i++) {
        if(isAdjacentNode(i) && !visit[i]) {
          stack.push(i);
          visit[i] = true;
        }
      }
    }
  }
  
  public boolean isAdjacentNode(int currentNode, int targetNode) {
    return graph[currentNode][targetNode] == 1;
  }

}

시간복잡도

• 인접 리스트: \(O(N+E)\) (\(N\): 정점 개수, \(E\): 간선 개수)
• 인접 행렬: \(O(N^2)\)

참고

2021.04.14 - [Algorithm] - [Algorithm] 그래프 (Graph)

2022.01.08 - [Algorithm] - [Algorithm] BFS (Breath-First-Search, 너비 우선 탐색)

Heap Sort

• Heap 자료구조를 이용하여 정렬하는 방식
• Best case, Worst case 모두 시간 복잡도가 \(O(nlogn)\)
  • 그러나 대체로 Quick Sort보다 느림
• 불안정 정렬(unstable sort)
  • 안정 정렬(stable sort) : 비교하는 원소의 값이 같을 때, input 순서대로 정렬

• 

Heap (약식)

• 최댓/최솟값을 찾는 연산을 빠르게 하기위해 고안된 자료구조
• 완전 이진트리(Complete Binary Tree)
• 부모노드의 Key값은 항상 자식노드의 Key값보다 우선순위가 높음
• index i에 대해서
  • 왼쪽 자식 노드의 index: \(i * 2 + 1\)
  • 오른쪽 자식 노드의 index: \(i * 2 + 2\)
  • 부모 노드의 index: \(i / 2\)
• 구조적으로 Tree이지만 배열로 표현가능
  •  

    

동작

Step 1. 배열을 Heap으로 만든다.

부모노드의 Key값은 항상 자식노드의 Key값보다 우선순위가 높다

Step 1-1. 

Step 1-2.

Step 1-3.

Step 2. 첫번째 index와 마지막 index를 swap 후 heap size를 1 줄인다.

Step 2-1.

Step 2-2.

Step 2-3.

Step 2-4.

Step 2-5.

Step 2-6.

코드

public class Sort {
	
    public void heapSort(int[] arr) {
    	int lastIndex = arr.length - 1;
        buildHeap(arr, lastIndex);
        
        for(int i = lastIndex; i > 0; i--) {
            swap(arr, 0, i);
            heapify(arr, 0, i-1);
        }
    }
    
    public void buildHeap(int[] arr, int lastIndex) {
    	int parent = (lastIndex - 1) / 2;
        
        for(int i = parent; i >= 0; i--) {
            heapify(arr, i, lastIndex);
        }
    }
    
    public void heapify(int[] arr, int parentIndex, int lastIndex) {
    	int leftChildIndex = parentIndex * 2 + 1;
        int rightChildIndex = parentIndex * 2 + 2;
        int largestIndex = parentIndex;
        
        if(leftChildIndex > lastIndex) {
        	return;
        }
        
        if(arr[leftChildIndex] > arr[largestIndex]) {
        	largestIndex = leftChildIndex;
        }
        
        if(rightChildIndex < lastIndex && arr[rightChildIndex] > arr[largestIndex]) {
        	largestIndex = rightChildIndex;
        }
        
        if(largestIndex != parentIndex) {
        	swap(arr, largestIndex, parentIndex);
            heapify(arr, largestIndex, lastIndex);
        }
    }
    
    public void swap(int[] arr, int index1, int index2) {
    	int temp = arr[index1];
        arr[index1] = arr[index2];
        arr[index2] = temp;
    }
}

왜 \(O(nlogn)\)일까?

Heap Sort의 의사코드를 보면 다음과 같다.

HeapSort(arr) {

    buildHeap(arr) // O(n)
    
    // O(nlogn)
    for( i = heapLastIndex ~ 0 ) {
        swap(arr, i, heapLastIndex)
        heapify(arr, 0, i - 1)
    }
}

Build Heap이 \(O(n)\)인 이유

for 구문이 \(O(nlogn)\)인 이유

Quick Sort

• 특정 원소(pivot)를 기준으로 왼쪽은 lower, 오른쪽은 upper 원소들을 두는 방식
• Merge Sort와 마찬가지로 Divide and Conquer 알고리즘
• 불안정 정렬(unstable sort)
  • 안정 정렬(stable sort): 비교하는 원소의 값이 같을 때 input 순서대로 정렬
• 평균적으로 \(O(nlogn)\)의 시간복잡도를 가지며, 매 Step마다 적어도 한 개의 원소는 반드시 자기 자리를 찾아가므로 매우 빠름
  • 하지만 최악의 경우에 \(O(n^2)\)의 시간복잡도를 가짐

  • 

동작

Step 1

Step 2

Step 3

Step 4

코드

public class Sort {
	
    public void quickSort(int[] arr, int first, int last) {
        if(first < last) {
            int pivot = partition(arr, first, last);
            quickSort(arr, first, pivot - 1);
            quickSort(arr, pivot + 1, last);
        }
    }
    
    public int partition(int[] arr, int first, int last) {
    	int pivot = arr[last];
        int i = first - 1;
        
        for(int j = first; j < last; j++) {
            if(arr[j] < pivot) {
            	swap(arr, ++i, j);
            }
        }
        swap(arr, i + 1, pivot);
        
        return i + 1;
    }
    
    public void swap(int[] arr, int index1, int index2) {
    	int temp = arr[index1];
        arr[index1] = arr[index2];
        arr[index2] = temp;
    }
}

왜 최악의 경우에는 \(O(n^2\)일까?

• 최선의 경우: 매 Step마다 원소가 중앙에 위치되어서 반으로 나누어지는 경우

• 최악의 경우: 매 Step마다 원소가 끝에 위치되어서 1 : 9 로 나누어지는 경우 (이미 정렬된 배열)

그래서 pivot을 선택하는 여러 variation 기법이 존재한다. (Randomized Quick Sort 등..)