# 개요
최단 경로 문제 정리
단어가 좀 혼용될 수 있다
- Ex) 노드==정점 / 간선==엣지
# 최단 경로 문제
가중치가 있는 방향/무방향 그래프에서 두 노드 사이의 가장 짧은 경로를 찾는 문제
# 최단 경로 문제의 유형
Single-Source / Single-Destination (One - to - All)

- 하나의 출발 노드로부터 다른 모든 노드까지의 최단 경로를 찾는 문제
- 모든 노드로부터 하나의 목적지 노드까지의 최단 경로를 찾는 문제
- 방향을 뒤집으면 서로 같아지기 때문에 사실상 같은 유형으로 본다.
- Dijkstra 알고리즘, Bellman Ford 알고리즘
All-Pairs (All - to - All)
- 모든 노드 쌍에 대하여 최단 경로를 찾는 문제
- Floyd-Warshall 알고리즘
# 최단경로와 음수 가중치
Dijkstra 알고리즘은 음수 가중치가 있을 경우 작동하지 않는다.
Bellman-Ford와 Floyd-Warshall 알고리즘은 음수 사이클이 없다는 가정하에 음수 가중치가 있어도 작동한다.
음수 사이클

음수 사이클이 있으면 최단 경로가 정의되지 않는다.
- 사이클의 합이 음수라면 계속 사이클을 돌게 되고 결국 합이 -∞되어 최단 경로를 찾을 수 없다.
- 단, 그래프 내에 음수 사이클이 있어도 그 사이클이 목적지까지 가는 경로에 없다면 상관없다.
# 최단 경로 문제의 기본 특성

1. 최단 경로의 어떤 부분 경로 역시 최단 경로이다. (Optimal SubStructure → DP)
- 위 경로가 u → v의 최단 경로라면, x → y의 경로 또한 최단 경로이다.
증명 (귀류법)

- 만약 더 짧은 경로(x → y)가 있다고 가정해보자
- 이 경로가 더 짧다면 u → v의 최단 경로는 u → v가 아니라 x → y를 거쳐가는 u → x → y → v가 될 것이다.
- 이것은 처음 가정(u →v 가 최단 경로라면)의 모순이 된다.
- 그러므로 최단 경로의 부분 경로도 최단 경로이다.
2. 최단 경로는 사이클을 포함하지 않는다.
# Single-Source 최단 경로 문제
음수 사이클이 없는 가중치 방향 그래프 G = (V, E)와 출발 노드 S에서 각 노드 v에 대하여 다음을 계산한다.
- d[v] (distance estimation): 출발 노드 S로부터 각 노드v에 대하여 현재까지 알고 있는 최단 경로의 길이 (→ 알고리즘이 진행됨에 따라 갱신 된다.)
- 처음에는 d[S] = 0, 각 d[v]들은 ∞으로 초기화한다.
- S는 출발 노드이고, 음수 사이클이 없으므로 가장 작은 값인 0
- 그 외의 다른 노드들 v는 아직 탐색 시작을 안했으므로 ∞
- 알고리즘이 수행됨에 따라 d[v]가 점점 감소하며 최종적으로 d[v]값이 S → v의 최단 경로 길이가 된다.
- 처음에는 d[S] = 0, 각 d[v]들은 ∞으로 초기화한다.
- π[v] (predecessor): S에서 v까지의 최단 경로 상에서 v의 직전 노드
- 처음에는 π[v]와 π[S]는 null로 초기화
- 출발 노드S의 이전 노드는 없으므로 null
- 다른 노드들 v는 아직 탐색 시작을 안했으므로 null
- 최단경로의 길이 외에 그 경로 자체를 요구할 수 있으므로 이전 노드를 기록하며 역추적한다.
- 처음에는 π[v]와 π[S]는 null로 초기화
기본 연산: Relaxation
1. d[u] = 5, d[v] = 9, w(u,v) = 2(간선 u → v의 가중치 값)인 상황
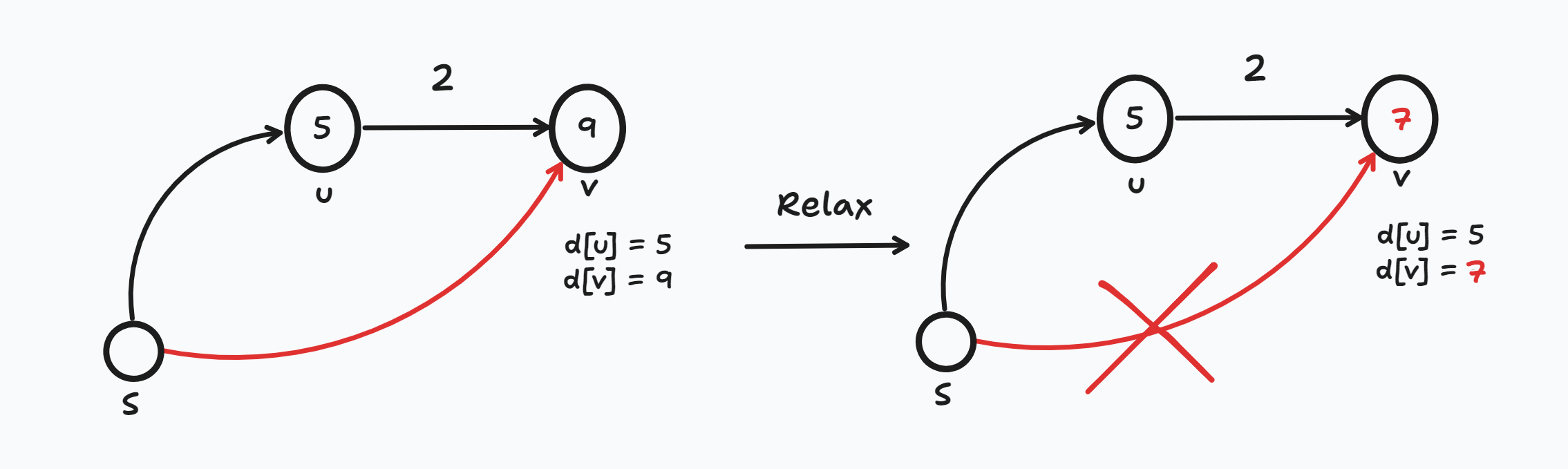
- d[v]는 "현재까지 알고 있는" S → v의 최단 경로 길이 이므로 Relaxation 연산에 따라 갱신 될 수 있다.
- 기존에 알고 있는 S → v의 최단 경로는 S → v로 d[v] = 9 였는데 더 짧은 경로인 S → u → v경로를 발견했으므로 d[v] = d[u] + w(u,v)로 갱신한다 (9 > 5+2)
2. d[u] = 5, d[v] = 6, w(u,v) = 2인 상황
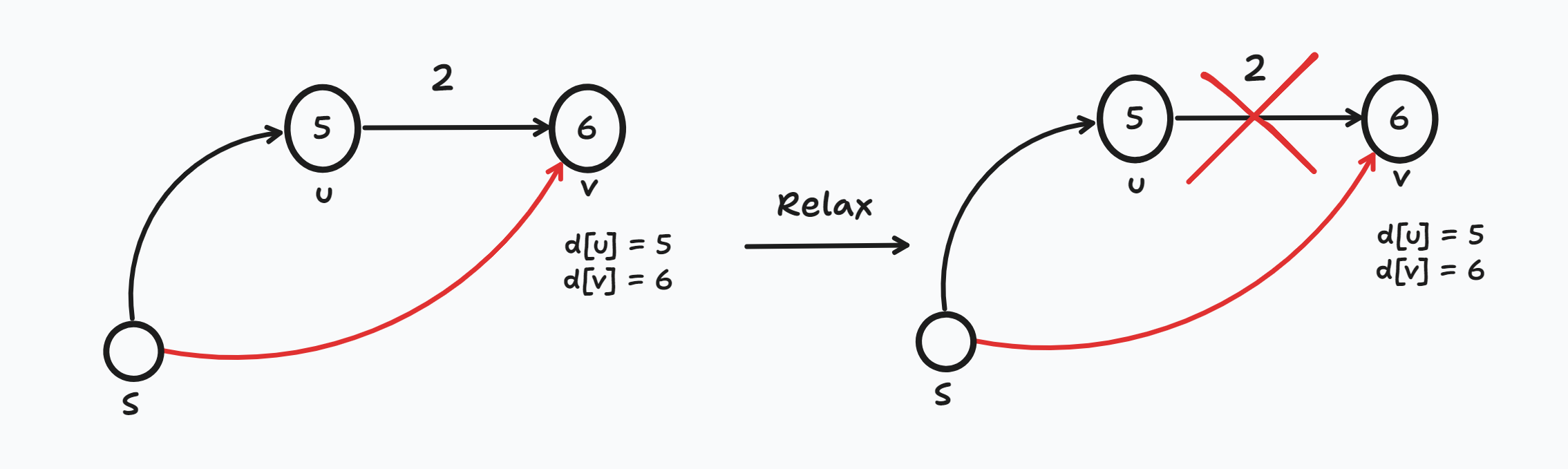
- Relaxation 연산을 했지만 기존 최단 경로인 S → v d[v]가 더 짧은 경로이므로 갱신하지 않는다.
Relaxtaion 의사 코드
Relax(u, v, w) {
if(d[v] > d[u] + w(u,v))
then d[v] ← d[u] + w(u,v)
π[v] ← u
}
대부분의 Single-Source 최단 경로 알고리즘의 기본 구조
- 초기화: d[S] = 0, 노드 v에 대해 d[v] = ∞, π[v]=null
- 간선들에 대해서 반복적인 Relaxtation 연산
의사 코드
Generic-Single-Source(G, w, S) {
Init(G, S)
Repeat
for each edge(u,v)
Relax(u,v,w)
until there is no change
}- 의문: 이렇게 반복하면 최단 경로가 정말 찾아질까?
- 의문: 찾아진다면 몇 번 반복해야 찾아질까?
증명
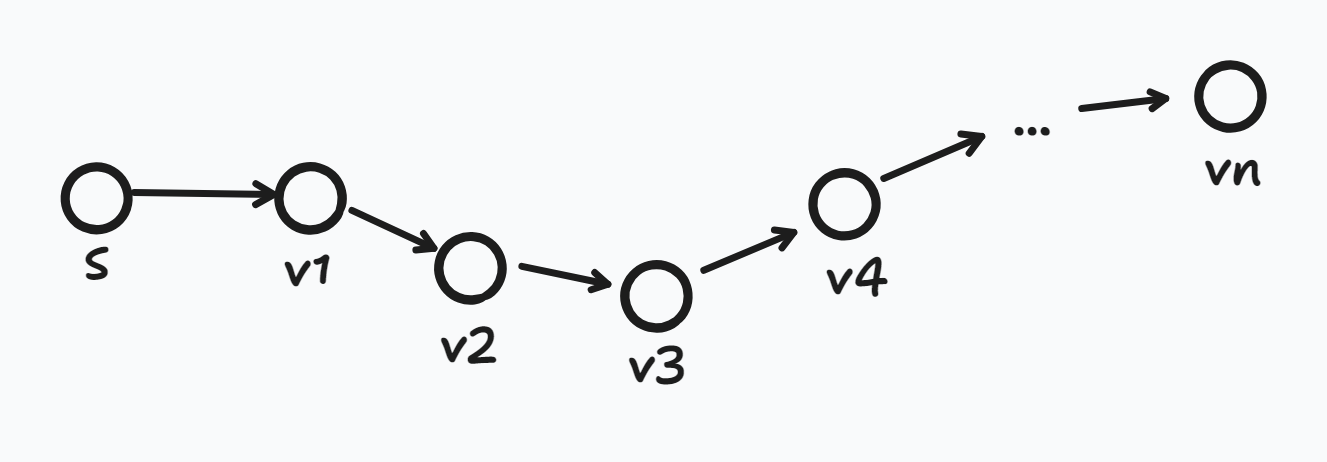
- 가정: N개의 정점에서, S → vn 경로가 최단 경로라면 이 경로에 포함된 간선의 개수는 최대 N-1개이다.
- 첫 번째 Round
- 모든 간선들에 대해 Relax연산을 하고, d[S] = 0, d[v1]이 ∞에서 d[S] + w(S, v1)을 통해 갱신 된다.
- S → vn까지의 최단 경로의 부분 경로 역시 최단 경로이므로 갱신 된 d[v1]이 곧 최단 경로가 된다.
- 두 번째 Round
- 모든 간선들에 대해 Relax연산을 하고, d[v2]이 ∞에서 d[v1] + w(v1, v2)을 통해 갱신 된다.
- 마찬가지로 갱신 된 d[v1]이 곧 최단 경로가 된다.
- 반복하면 d[vn]은 n-1번째 Round에 최단 경로가 된다.
- 즉 노드의 개수가 N개라면 N-1번의 반복으로 모든 노드의 최단 경로를 구할 수 있다.
직관적으로 봐도 vn까지 최단 경로의 간선 수는 최대 N-1라는 것을 생각할 수 있는데
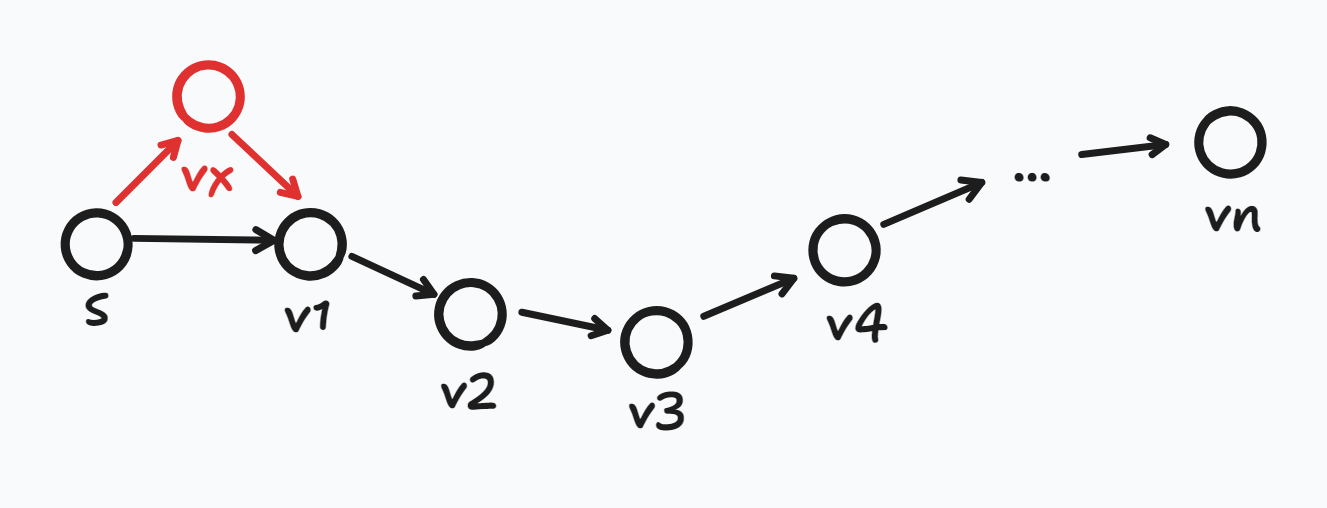
- vx를 거쳐가는 더 짧은 경로가 있다면? → 그럼 그 경로가 최단 경로가 되며, N개의 정점에서 N+1개의 정점이 되었다. 그러므로 간선의 개수는 최대 N개가 될 것이다.
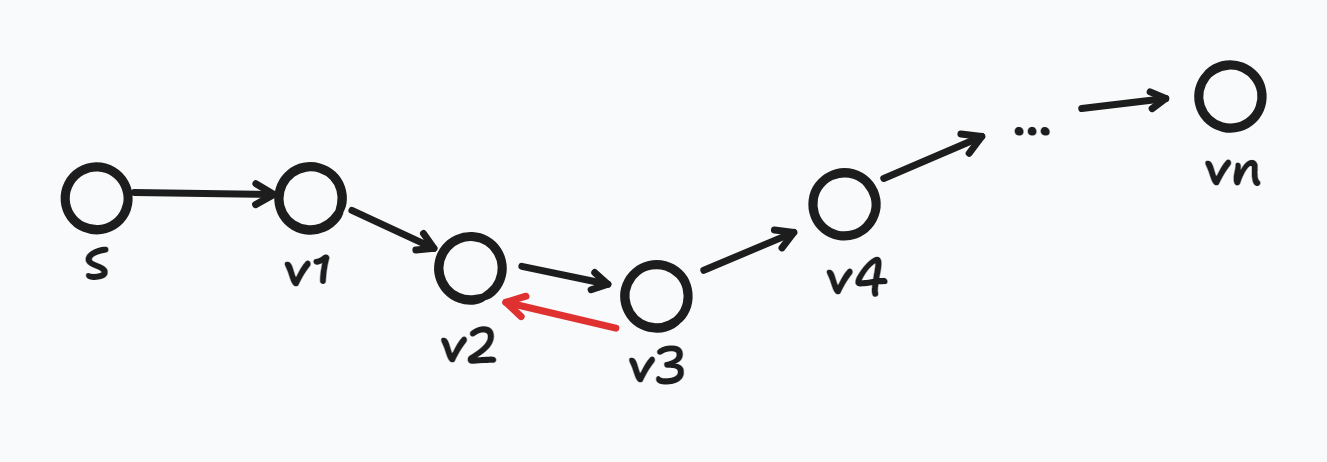
- v2 → v3 → v4 경로를 통해 가는 것보다 v3 → v2 갔다가 다시 v2 → v3으로 가는 것이 더 빠르다면? → 그 자체로 음수 사이클이 생긴다는 뜻이며 음수 사이클이 없다는 전제에 모순된다.
Worst Case
시간 복잡도: O(n^3) → 효율적인 알고리즘이라고 할 수 없다.
다음과 같은 상황을 보자
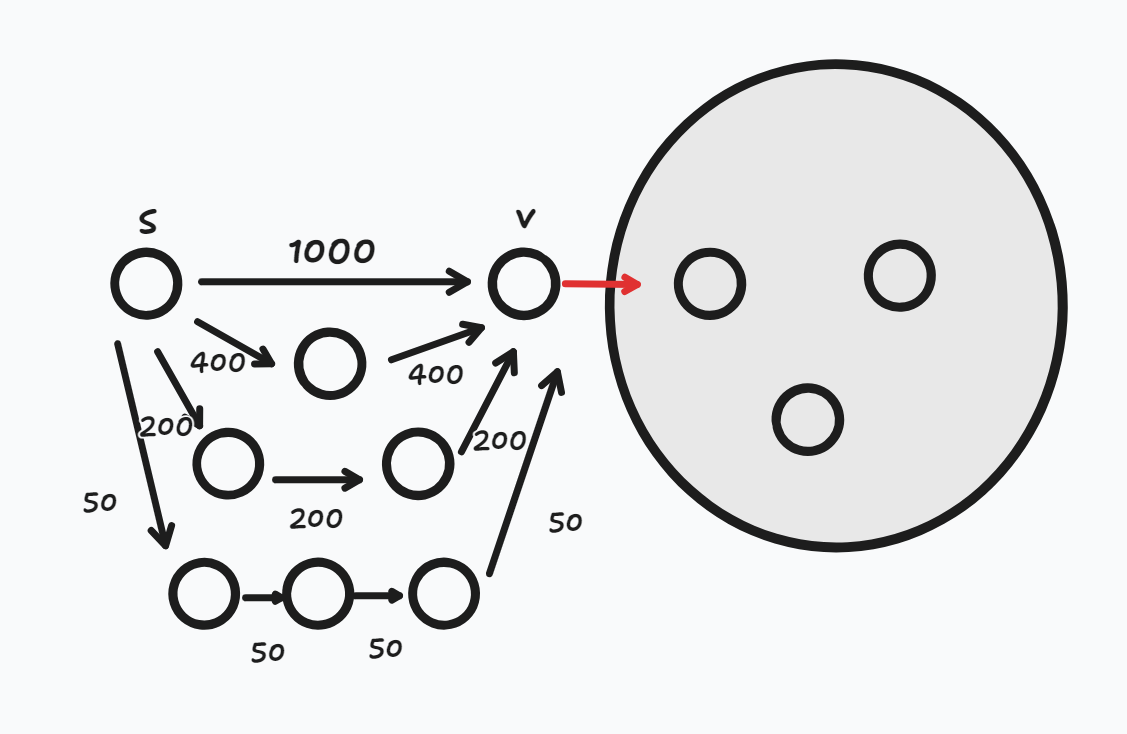
- 첫 번째 Round에서 간선들을 어떠한 순서로 Relax 연산을 하다보니 d[v] = 1000이 되었다.
- 두 번째 Round에서 간선들을 어떠한 순서로 Relax 연산을 하다보니 d[v] = 800이 되었다.
- 최악의 상황은 마지막 Round에서 d[v] = 200으로 갱신 되고 이것이 최단 경로라는 것을 알게 되었을 때이다. 그제서야 v 이후의 노드들에 대한 최단 경로를 알 수 있게 된다.
- 하지만 처음부터 가중치가 50인 경로로 Relax를 했다면 더 빠르게 최단 경로를 찾을 수 있지 않았을까?
- Dijkstra 알고리즘으로 해결
- 최악의 경우 시간 복잡도가 O(n^3)인데도 사용하는 이유는 가중치가 음수일 때도 동작하고, 음수 사이클 여부를 알 수 있기 때문이다.
# Reference
권오흠 교수님 유튜브 및 강의자료
'Algorithm' 카테고리의 다른 글
| [Algorithm] Bellman-Ford(벨만포드) 알고리즘 (1) | 2024.01.25 |
|---|---|
| [Alogorithm] Dijkstra(다익스트라) 알고리즘 (1) | 2024.01.24 |
| [Algorithm] Prim(프림) 알고리즘 (0) | 2022.01.16 |
| [Algorithm] Krsukal (크루스칼) 알고리즘 (0) | 2022.01.16 |
| [Algorithm] MST (Minimum Spanning Tree, 최소 신장 트리) (0) | 2022.01.16 |
