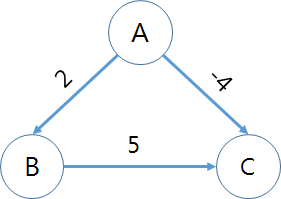
그래프 순회

• 그래프에서 임의의 한 정점에서 출발하여 모든 정점을 한번씩 방문하는 작업
• 탐색하는 동안 이미 방문한 정점이 있을 수 있으므로 방문했다는 표시를 하여 중복방문을 피한다.
• 대표적으로 DFS, BFS가 있다.

BFS (Breath-First-Search): 너비 우선 탐색

• 출발노드에서 인접한 노드(형제노드)를 먼저 탐색하는 방식
• 가중치가 없는 그래프에서 최단경로를 찾을 때 사용한다.
• 일반적으로 Queue를 이용하여 구현한다.

동작방식

1. 시작정점을 방문하여 큐에 삽입한다.
2. 큐에서 정점을 꺼내 정점에서 인접한 정점중, 방문하지 않은 정점들을 방문하여 큐에 삽입한다.
3. 모든 정점을 반복할 때까지 반복한다.

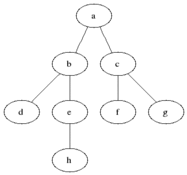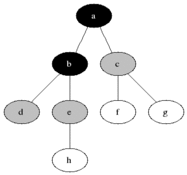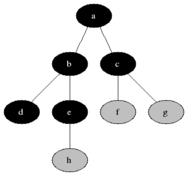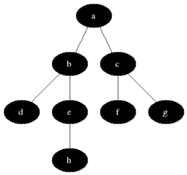
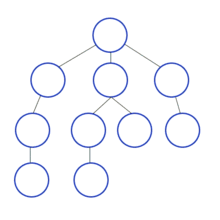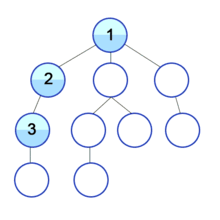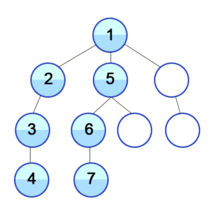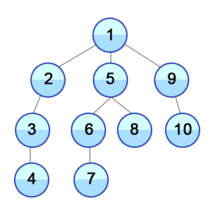
Visualize

E노드에서 더이상 간선이 없으므로 그냥 큐에서 꺼내는것으로 끝이다

G노드에서 더이상 간선이 없으므로 그냥 큐에서 꺼내는것으로 끝이다. H노드와 I노드도 마찬가지이다.

코드

의사코드

BFS(graph, start_node) {
  Queue q;
  boolean[] visit;
  
  q.add(start_node);
  visit[start_node] = true;
  
  while(!q.isEmpty()) {
    current_node = q.pop();
    for(adjacent_node to current_node) {
      if(!visit[adjacent_node]) {
        visit[adjacent_node] = true;
        q.add(adjacent_node);
      }
    }
  }
}

코드 - Queue (Java)

class BFS_Queue {
  private int[][] graph;
  private boolean[] visit;
  
  public BFS_Queue() {
    this.graph = {
      {0, 1, 1, 1, 0, 0, 0, 0, 0},
      {1, 0, 0, 0, 1, 0, 0, 0, 0},
      {1, 0, 0, 0, 0, 1, 1, 0, 0},
      {1, 0, 0, 0, 0, 0, 0, 1, 0},
      {0, 1, 0, 0, 0, 0, 0, 0, 0},
      {0, 0, 1, 0, 0, 0, 0, 0, 1},
      {0, 0, 1, 0, 0, 0, 0, 0, 0},
      {0, 0, 0, 1, 0, 0, 0, 0, 0},
      {0, 0, 0, 0, 0, 1, 0, 0, 0},
    };
    this.visit = new boolean[graph.length];
  }
  
  public void bfs(startNode) {
    Queue<Integer> queue = new LinkedList();
    
    queue.add(startNode);
    visit[startNode] = true;
    
    while(!queue.isEmpty()) {
      int currentNode = queue.poll();
      
      for(int i = 0; i < graph[currentNode].length; i++) {
        if(isAdjacentNode(currentNode, i) && !visit[i]) {
          visit[i] = true;
          queue.add(i);
        }
      }
    }
  }
  
  public boolean isAdjacentNode(int currentNode, int targetNode) {
    return graph[currentNode][targetNode] == 1;
  }
}

시간 복잡도

• 인접 리스트: \(O(N+E)\) (\(N\): 정점 개수, \(E\): 간선 개수)
• 인접 행렬: \(O(N^2)\)

참고

2021.04.14 - [Algorithm] - [Algorithm] 그래프 (Graph)

2022.01.08 - [Algorithm] - [Algorithm] DFS (Depth-First-Search, 깊이 우선 탐색)

그래프 순회

• 그래프에서 임의의 한 정점에서 출발하여 모든 정점을 한번씩 방문하는 작업
• 탐색하는 동안 이미 방문한 정점이 있을 수 있으므로 방문했다는 표시를하여 중복방문을 피한다.
• 대표적으로 DFS와 BFS가 있다.

DFS (Depth-First-Search): 깊이 우선 탐색

• 출발노드에서 하위노드(자식노드)를 먼저 탐색하는 방식
• 일반적으로 Stack이나 Recursive를 이용하여 구현한다.

동작방식

1. 시작노드에서 간선을 따라 다음노드로 방문한다.
2. 더이상 탐색할 간선이 없다면 역추적(Backtracking)을 통해 이전노드로 이동하여 아직 탐색하지 않은 간선을 참색한다.
3. 모든 노드를 탐색할 때까지 반복한다.

Visualize

E노드에서 더이상 이동 할 간선이 없으므로 역추적으로 통해 B노드로 이동, B노드에서도 마찬가지로 더이상 이동할 간선이 없으므로 A노드로 이동 후 다음 간선인 (A,C)을 통해 C노드로 이동

F노드에서 더이상 이동할 간선이 없으므로 역추적을 통해 C노드로 이동, C노드에서 다음 간선인 (C,G)을 통해 G노드로 이동

I노드에서 더이상 이동할 간선이 없으므로 역추적을 통해 G노드로 이동, G노드에서도 마찬가지로 C노드로 이동, C노드에서도 마찬가지로 A노드로 이동, A노드에서 다음 간선인 (A,D)를 통해 D노드로 이동

코드

의사코드

DFS(graph, current_node, visit) {
  visit[current_node] = true
  
  for( adjacent_node to current_node) {
    if(!visit[adjacent_node]) {
      DFS(graph, adjacent_node, visit)
    }
  }
}

코드 - Recursive (Java)

class DFS_Recursive {

  private int[][] graph;
  
  private boolean[] visit;
  
  public DFS_Recursive() {
    this.graph = {
      {0, 1, 1, 1, 0, 0, 0, 0, 0},
      {1, 0, 0, 0, 1, 0, 0, 0, 0},
      {1, 0, 0, 0, 0, 1, 1, 0, 0},
      {1, 0, 0, 0, 0, 0, 0, 1, 0},
      {0, 1, 0, 0, 0, 0, 0, 0, 0},
      {0, 0, 1, 0, 0, 0, 0, 0, 1},
      {0, 0, 1, 0, 0, 0, 0, 0, 0},
      {0, 0, 0, 1, 0, 0, 0, 0, 0},
      {0, 0, 0, 0, 0, 1, 0, 0, 0},
    };
    visit = new boolean[graph.length];
  }
  
  public void dfs(currentNode) {
    visit[currentNode] = true;
    
    for(int i = 0; i < graph[currentNode].length; i++) {
      if(isAdjacentNode(currentNode, i) && !visit[i]) {
        dfs(i);
      }
    }
  }
  
  public boolean isAdjacentNode(int currentNode, int targetNode) {
    return graph[currentNode][targetNode] == 1;
  }

}

코드 - Stack

class DFS_Stack {

  private int[][] graph;
  
  private boolean[] visit;
  
  public DFS_Stack() {
    this.graph = {
      {0, 1, 1, 1, 0, 0, 0, 0, 0},
      {1, 0, 0, 0, 1, 0, 0, 0, 0},
      {1, 0, 0, 0, 0, 1, 1, 0, 0},
      {1, 0, 0, 0, 0, 0, 0, 1, 0},
      {0, 1, 0, 0, 0, 0, 0, 0, 0},
      {0, 0, 1, 0, 0, 0, 0, 0, 1},
      {0, 0, 1, 0, 0, 0, 0, 0, 0},
      {0, 0, 0, 1, 0, 0, 0, 0, 0},
      {0, 0, 0, 0, 0, 1, 0, 0, 0},
    };
    visit = new boolean[graph.length];
  }
  
  public void dfs(startNode) {
    Stack<Integer> stack = new Stack();
    
    stack.push(startNode);
    visit[startNode] = true;
    
    while(!stack.isEmpty()) {
      int currentNode = stack.pop();
      
      for(int i = 0; i < graph[currentNode].length; i++) {
        if(isAdjacentNode(i) && !visit[i]) {
          stack.push(i);
          visit[i] = true;
        }
      }
    }
  }
  
  public boolean isAdjacentNode(int currentNode, int targetNode) {
    return graph[currentNode][targetNode] == 1;
  }

}

시간복잡도

• 인접 리스트: \(O(N+E)\) (\(N\): 정점 개수, \(E\): 간선 개수)
• 인접 행렬: \(O(N^2)\)

참고

2021.04.14 - [Algorithm] - [Algorithm] 그래프 (Graph)

2022.01.08 - [Algorithm] - [Algorithm] BFS (Breath-First-Search, 너비 우선 탐색)

참고1 : 유튜브 (권오흠 교수, 2015 봄학기 알고리즘)

참고2 : (다양한 예제로 학습하는) 데이터 구조와 알고리즘 for java

1. 그래프 : G = (V, E)

1. 정의

• V : 정점(Vertex) 또는 노드(Node)들의 집합
• E : 간선,에지(Edge) 또는 링크(Link)라고 불리는 정점들의 쌍의 집합
• G = (V, E)

2. 종류

• 무방향(undirected) 그래프 vs 방향(directed) 그래프
  • 방향이 없는 그래프 vs 방향이 있는 그래프
  • (u, v) == (v, u) vs (u, v) != (v,u)
  • vs
• 가중치 그래프(Weight Graph)
• 방향, 무방향 그래프에 관계없이 각 간선에 가중치(weight) 혹은 비용(cost)이 할당된 그래프
  • 

3. 용어

• 인접 정점 or 인접 노드 : 간선에 의해 연결된 정점
• 차수(degree) : 정점에 연결된 다른 정점의 개수
  • 진입 차수(in-degree) : 방향 그래프에서 외부 노드에서 들어오는 간선의 수
  • 진출 차수(out-degree) : 방향 그래프에서 외부 노드로 나가는 간선의 수
• 연결 그래프(connected Graph)
  • 무방향 그래프에서 두 노드 사이를 연결하는 경로(path)가 존재할 때 두 정점은 서로 연결되어 있다고 한다.
  • 그래프 안의 모든 정점이 연결되어 있을때 연결된 그래프라고 한다
  • 연결 요소

  • 

2. 그래프의 표현

1. 인접 행렬

• 

  • 두 정점 사이에 간선이 있을경우 1, 없을 경우 0으로 표현한다.
    • 가중치 그래프의 경우 0,1 대신 가중치로 표현한다.
  • 무방향 그래프의 경우 자기 자신을 기준으로 대칭이다. (A, B) == (B, A)
    • 방향 그래프의 경우 비대칭이다.
  • 저장공간 : O(n^2)
  • 어떤 노드 v에 인접한 모든 노드를 찾을 때 걸리는 시간 : O(n)
  • 어떤 간선 (u,v)가 존재하는지 검사할때 걸리는 시간 : O(1)
• 간단한 구현 코드 (무방향 그래프)

public class Graph {
    int[][] adjMatrix;
    int vertexCount;

    public Graph(int count) {
        vertexCount = count;
        adjMatrix = new int[vertexCount][vertexCount];
    }

    public void addEdge(int u, int v) {
        adjMatrix[u][v] = 1;
        adjMatrix[v][u] = 1;
    }

    public void removeEdge(int u, int v) {
        adjMatrix[u][v] = 0;
        adjMatrix[v][u] = 0;
    }

    public List<Integer> findAdjVertex(int u) {
        ArrayList<Integer> adjVertexList = new ArrayList<>();
        for(int i = 0; i<adjMatrix.length; i++) {
            if(adjMatrix[u][i] == 1) {
                adjVertexList.add(i);
            }
        }
        return adjVertexList;
    }

    public boolean isEdge(int u, int v) {
        return adjMatrix[u][v] == 1;
    }
}

2. 인접 리스트

• 

  • 정점 집합을 표현하는 하나의 배열과 각 정점마다 인접한 정점들의 리스트
  • 두 정점 사이에 간선이 있을 경우 리스트에 추가한다 (순서는 상관없다)
  • 저장 공간 : O(n+m)
    • n은 정점개수, m은 간선 개수이다.
    • 무방향 그래프의 경우 2m, 방향 그래프의 경우 m이지만, Big - O 표기법에서는 O(n+m)이다.
  • 어떤 노드 v에 인접한 모든 노드를 찾을 때 걸리는 시간 : O(degree(v))
    • v에 해당하는 리스트의 길이이다.
  • 어떤 간선 (u,v)가 존재하는지 검사할 때 걸리는 시간 : O(degree(u))
    • u에 대한 연결 리스트를 돌면서 v가 있는지 확인한다.
• 간단한 구현코드 (무방향 그래프)

public class Graph {
	List<Integer>[] adjList;
    int vertexCount;
    
    public Graph(int count) {
    	vertexCount = count;
        adjList = new List[vertexCount];
        for(int i = 0; i<vertexCount; i++) {
        	adjList[i] = new ArrayList<>();
        }
    }
    
    public addEdge(int u, int v) {
    	adjList[u].add(v);
        adjList[v].add(u);
    }
    
    public removeEdge(int u, int v) {
    	adjList[u].remove(adjList[u].indexOf(v));
        adjList[v].remove(adjList[v].indexOf(u));
    }
    
    public List<Integer> findAdjVertex(int u) {
    	return adjList[u];
    }
    
    public boolean isEdge(int u, int v) {
    	for(int i = 0; i < adjList[u].size(); i++) {
        	if(adjList[u].get(i) == v) {
            	return true;
            }
        }
        return false;
    }

}