Dev 일기장

1. 문제

https://www.acmicpc.net/problem/1944

문제 설명

세준이는 어느 날 획기적인 로봇을 한 개 개발하였다. 그 로봇은 복제 장치를 이용하면 자기 자신을 똑같은 로봇으로 원하는 개수만큼 복제시킬 수 있다. 세준이는 어느 날 이 로봇을 테스트하기 위하여 어떤 미로에 이 로봇을 풀어 놓았다. 이 로봇의 임무는 미로에 흩어진 열쇠들을 모두 찾는 것이다. 그리고 열쇠가 있는 곳들과 로봇이 출발하는 위치에 로봇이 복제할 수 있는 장치를 장착해 두었다.

N*N의 정사각형 미로와 M개의 흩어진 열쇠의 위치, 그리고 이 로봇의 시작 위치가 주어져 있을 때, 모든 열쇠를 찾으면서 로봇이 움직이는 횟수의 합을 최소로 하는 프로그램을 작성하여라. 로봇은 상하좌우 네 방향으로 움직이며, 로봇이 열쇠가 있는 위치에 도달했을 때 열쇠를 찾은 것으로 한다. (복제된 로봇이어도 상관없다) 하나의 칸에 동시에 여러 개의 로봇이 위치할 수 있으며, 로봇이 한 번 지나간 자리라도 다른 로봇 또는 자기 자신이 다시 지나갈 수 있다. 복제에는 시간이 들지 않으며, 로봇이 움직이는 횟수의 합은 분열된 로봇 각각이 움직인 횟수의 총 합을 말한다. 복제된 로봇이 열쇠를 모두 찾은 후 같은 위치로 모일 필요는 없다.

입력

첫째 줄에 미로의 크기 N(4 ≤ N ≤ 50)과 열쇠의 개수 M(1 ≤ M ≤ 250) 이 공백을 사이에 두고 주어진다. 그리고 둘째 줄부터 N+1째 줄까지 미로의 정보가 주어진다. 미로는 1과 0, 그리고 S와 K로 주어진다. 1은 미로의 벽을 의미하고, 0은 지나다닐 수 있는 길, S는 로봇이 출발하는 위치, K는 열쇠의 위치가 주어진다. S는 1개, K는 M개가 주어진다. S와 K에서만 복제를 할 수 있음에 유의한다. 미로는 벽으로 둘러쌓여 있는 형태이다. 즉, 모든 테두리는 벽이다.

출력

첫째 줄에 모든 로봇이 움직인 횟수의 총 합을 출력한다. 모든 열쇠를 찾는 것이 불가능한 경우 횟수 대신 첫째 줄에 -1을 출력하면 된다.

2. 어떻게 풀까

• 각 Key와 Start 지점에서 로봇이 복제 될 수 있다는 것은 A지점에서 출발해서 B지점으로 가는 거리가 Start 지점에서 B지점으로 가는 거리가 더 가까울 수 있다는 뜻이다.
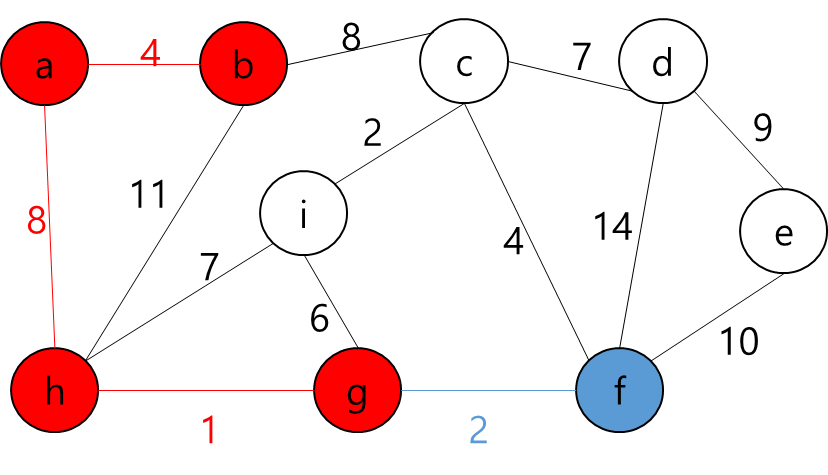
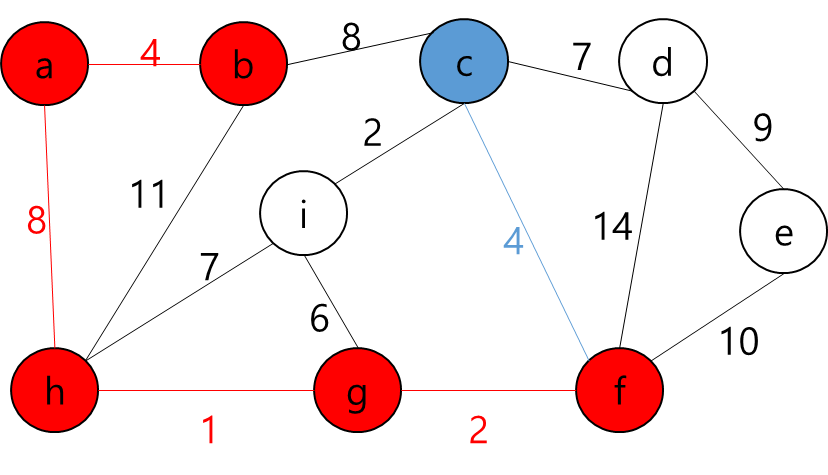
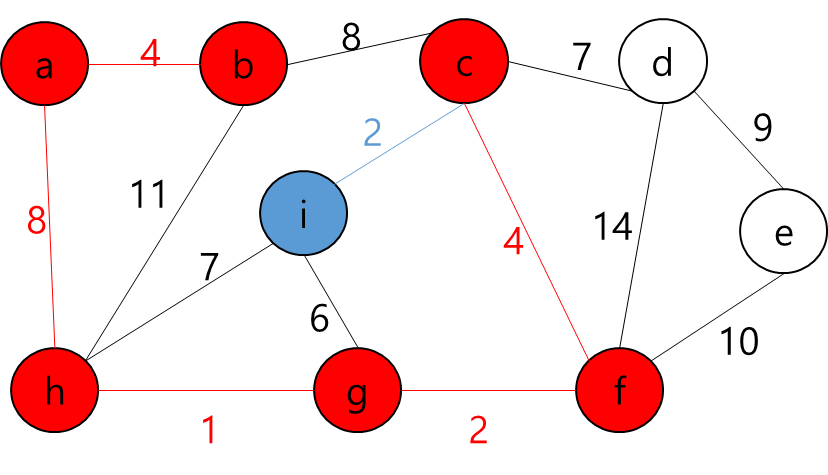
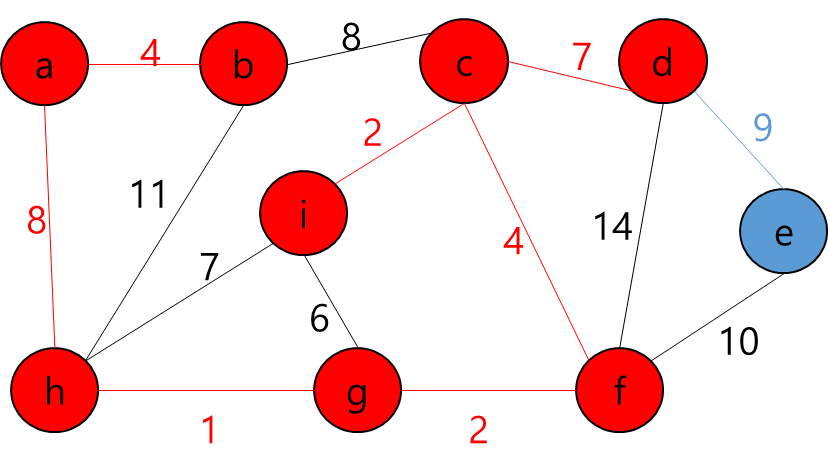
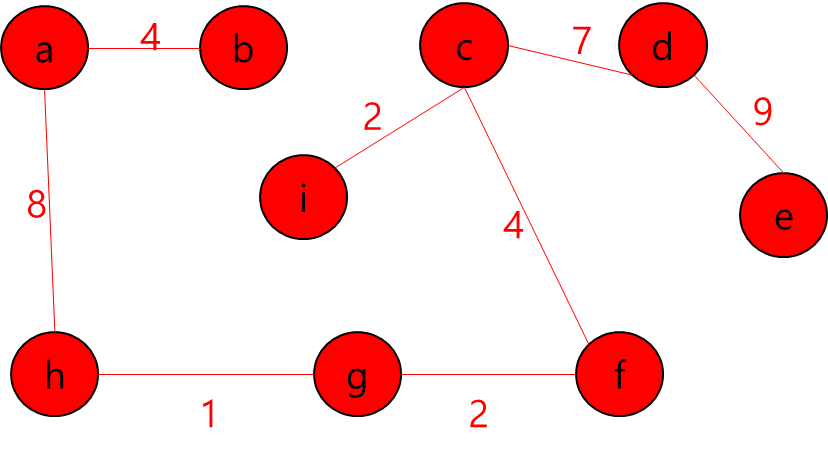
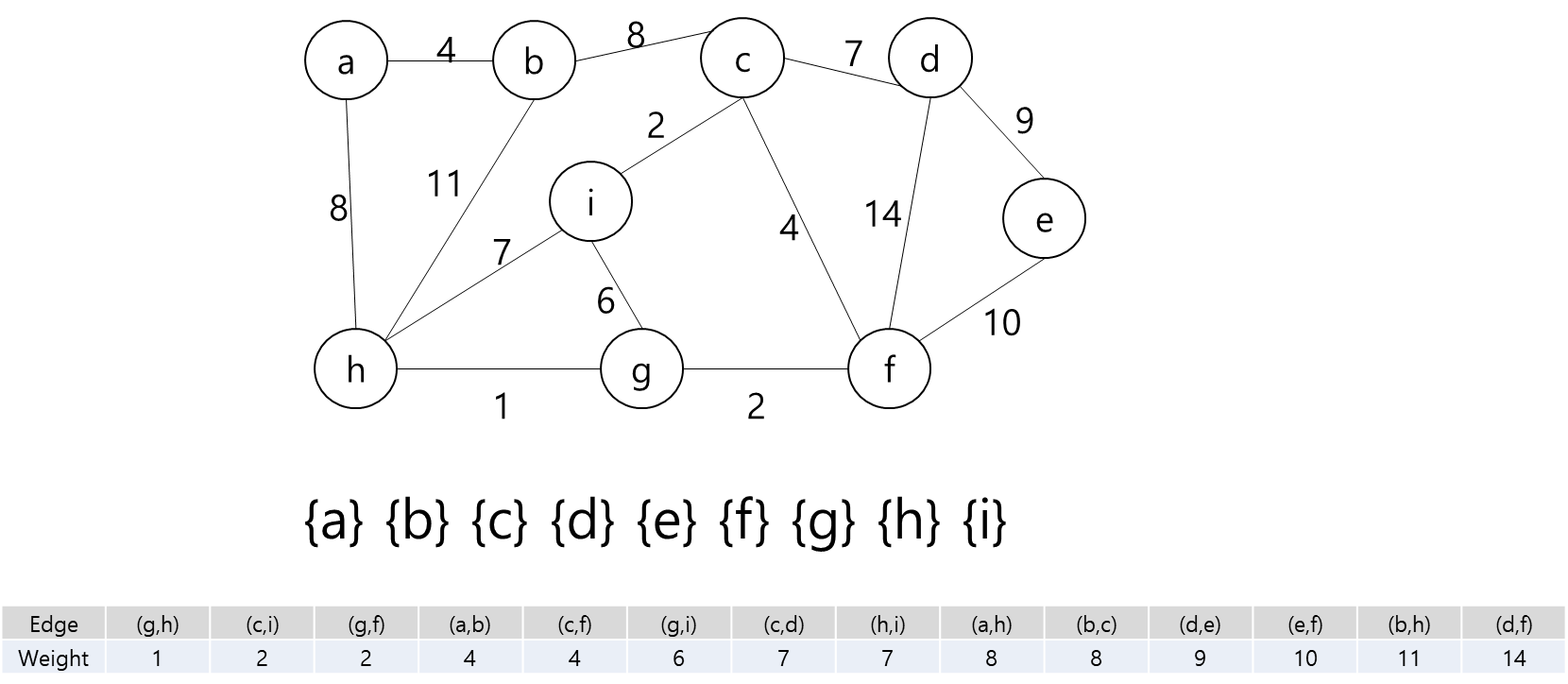
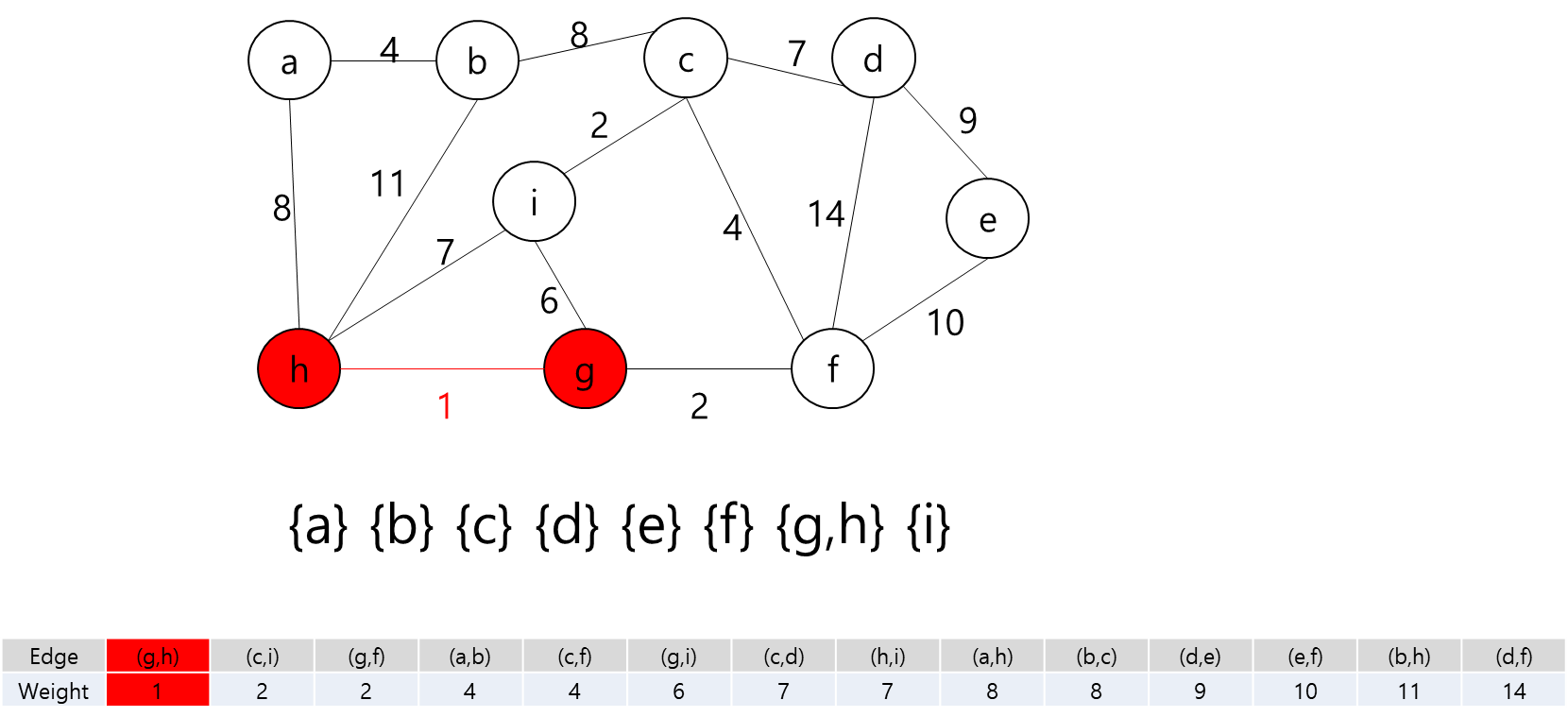
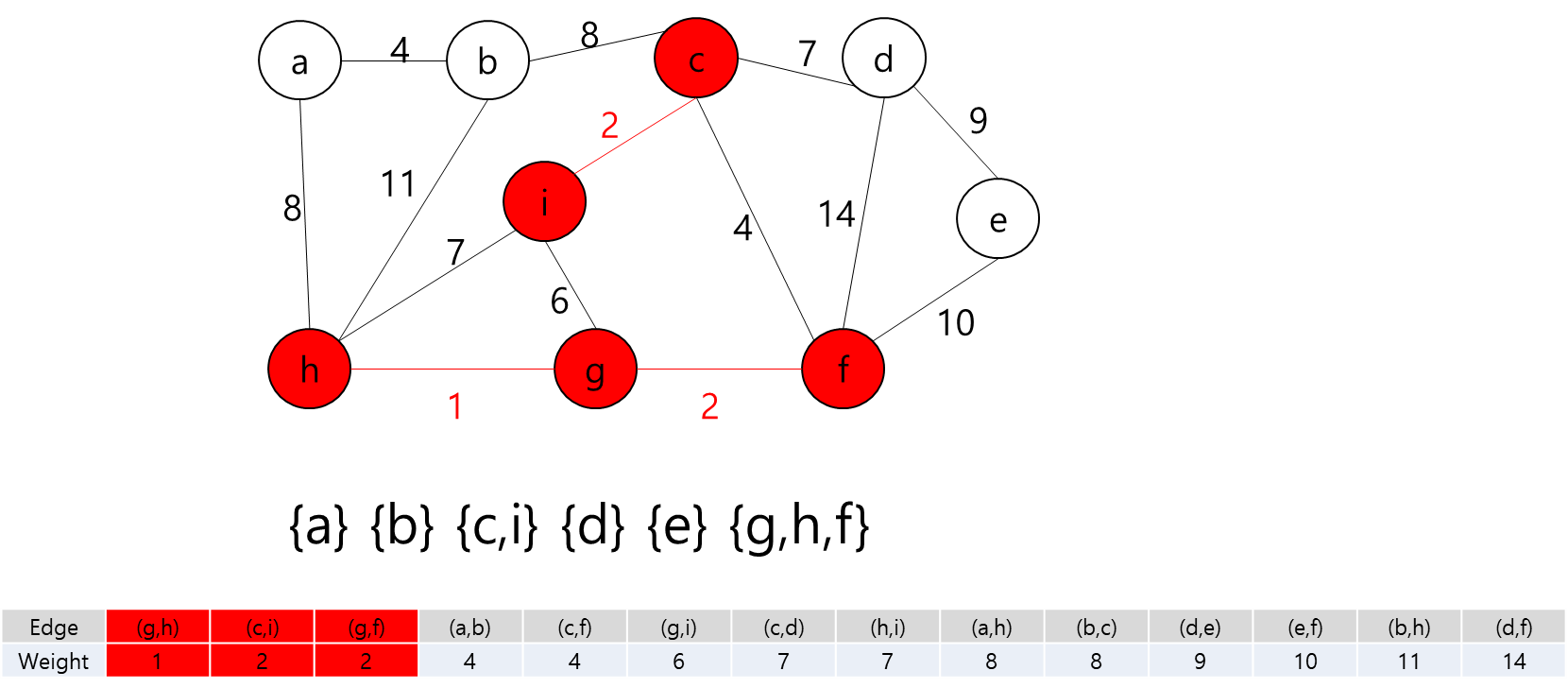
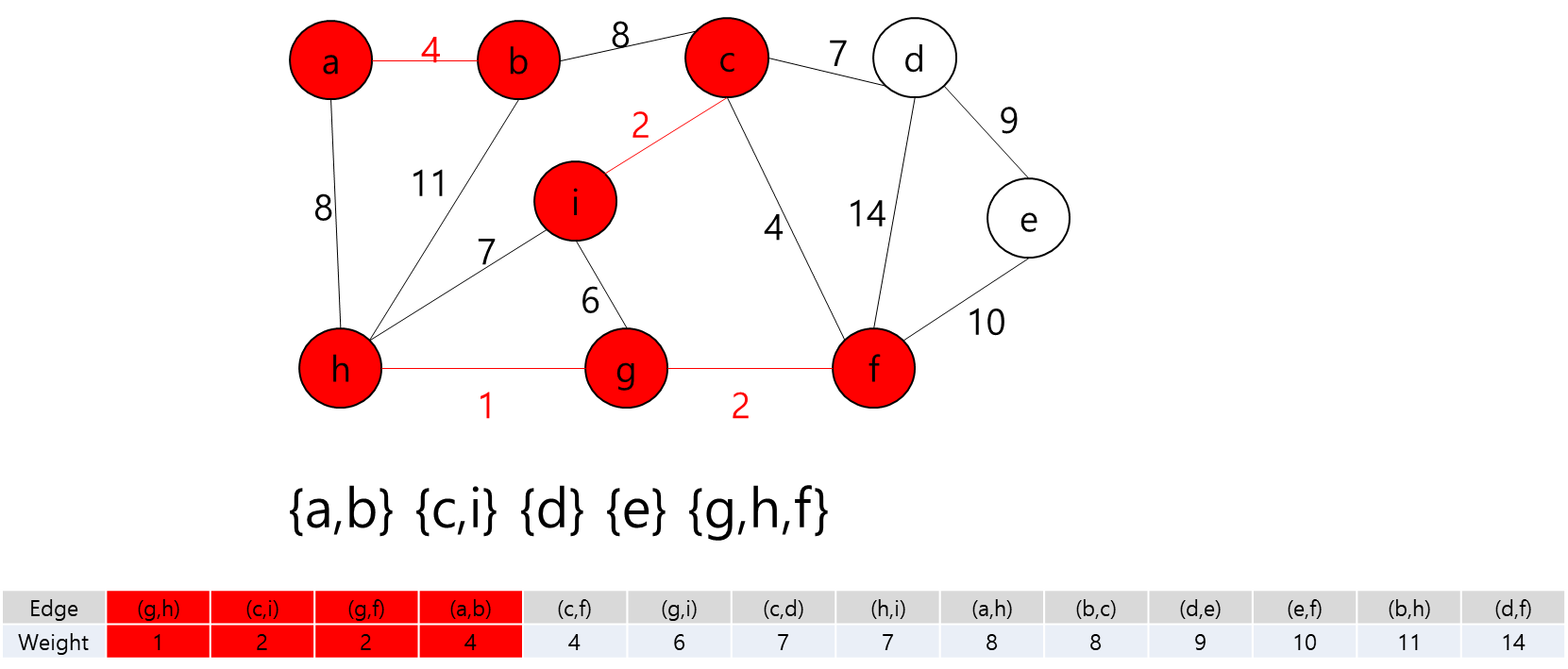
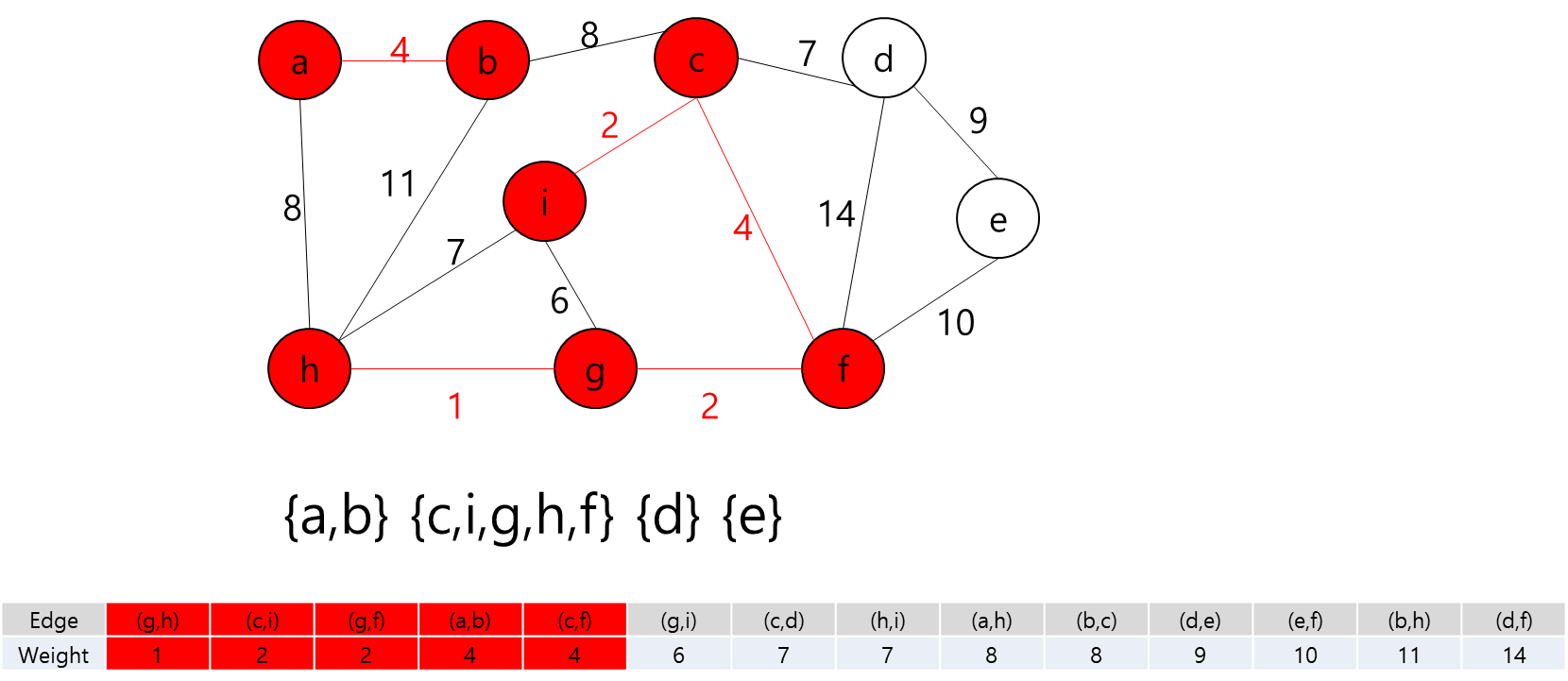
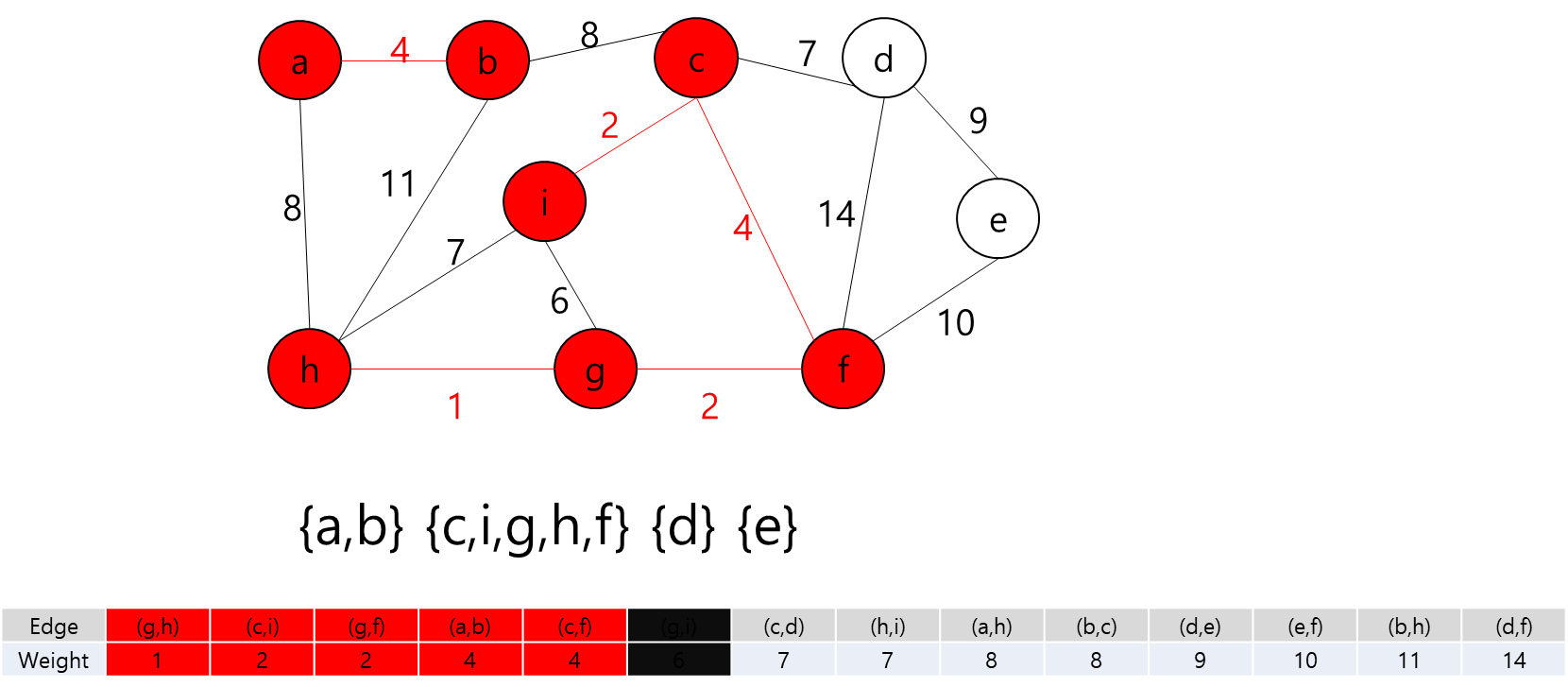
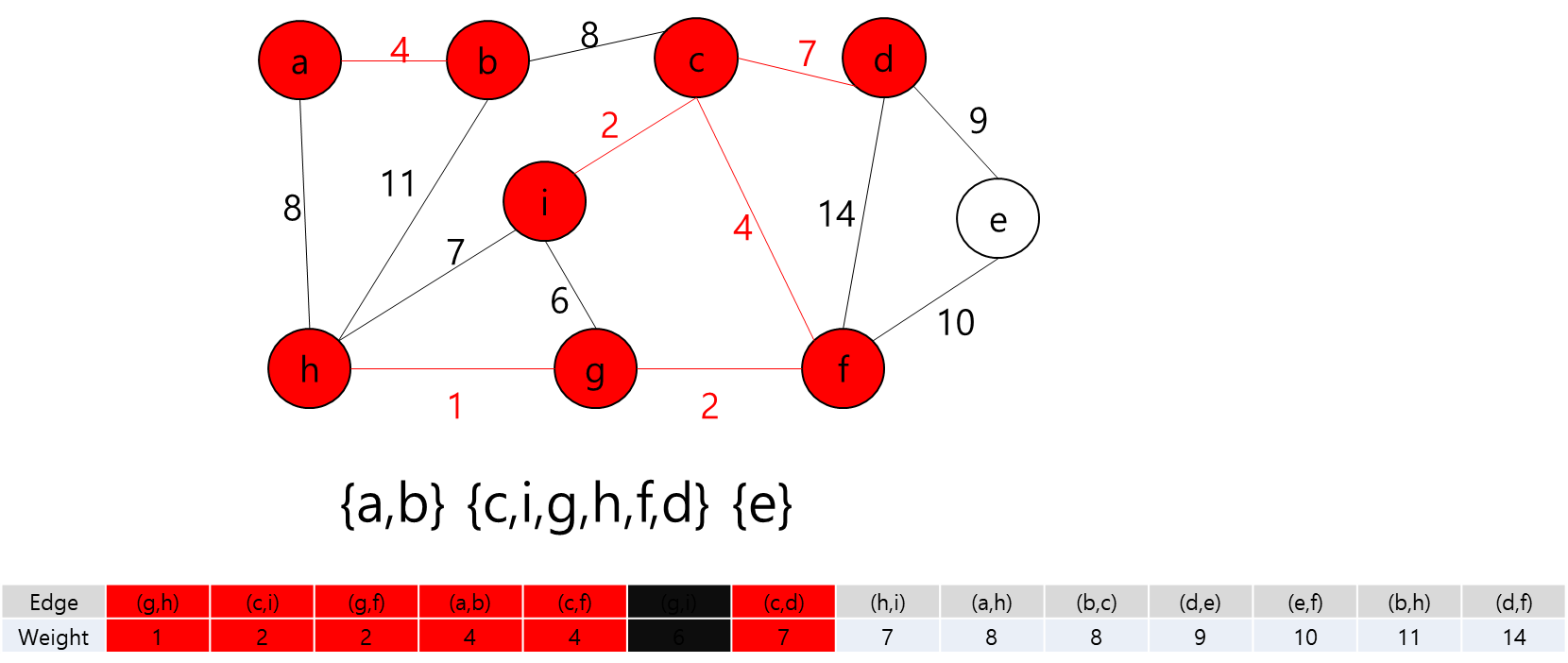
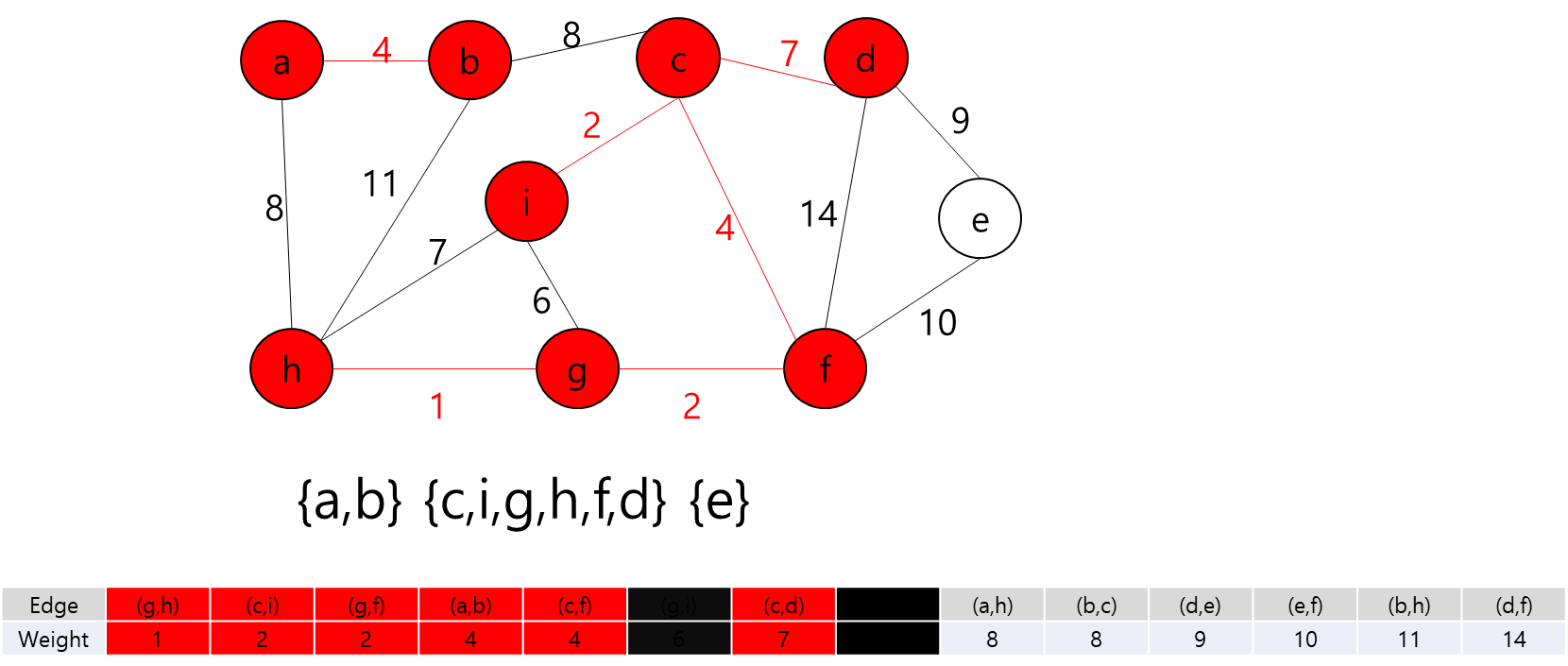
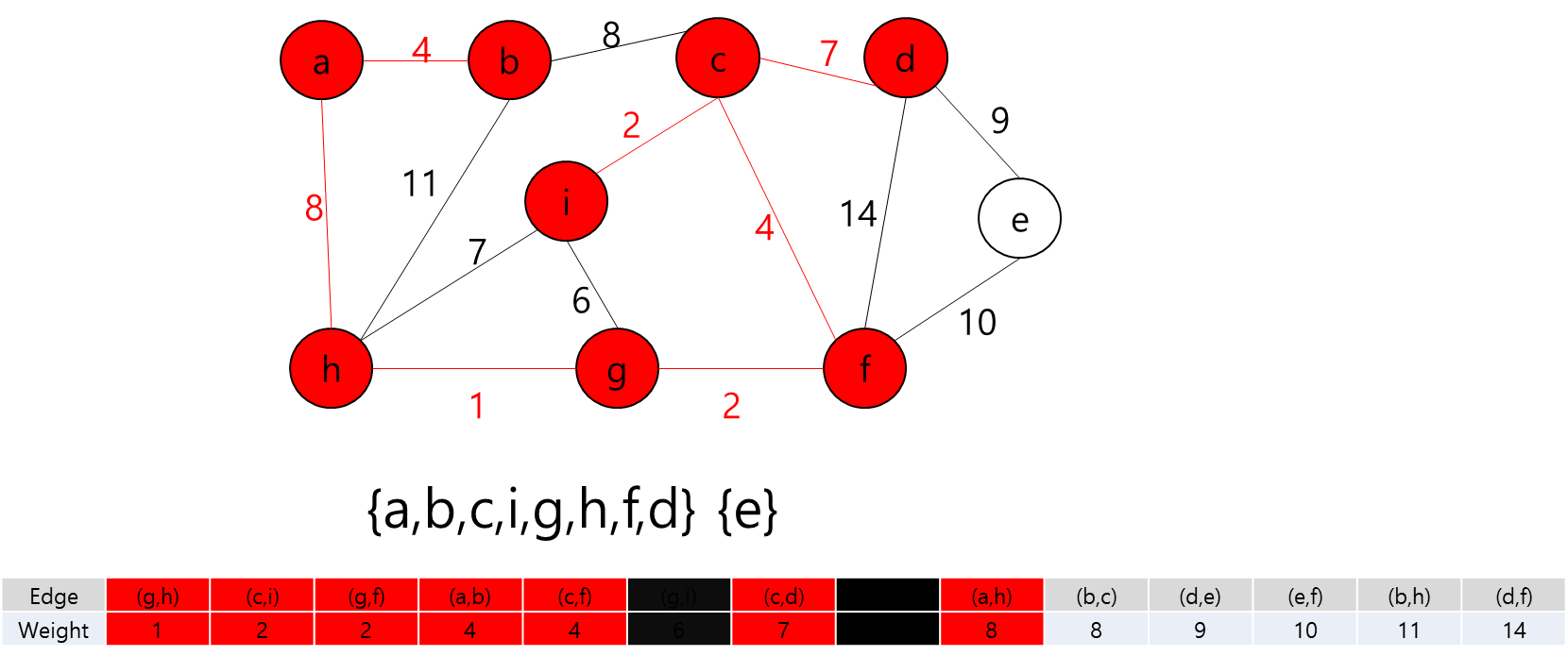
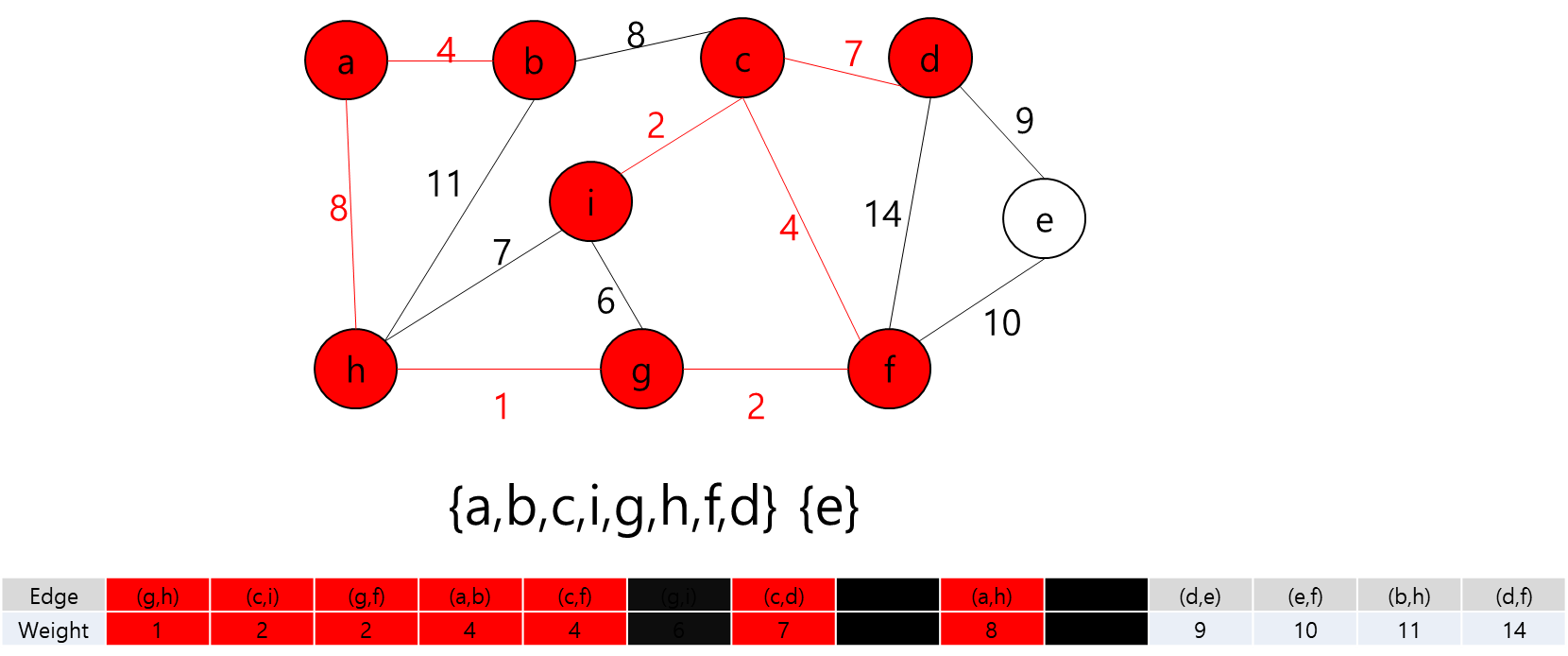
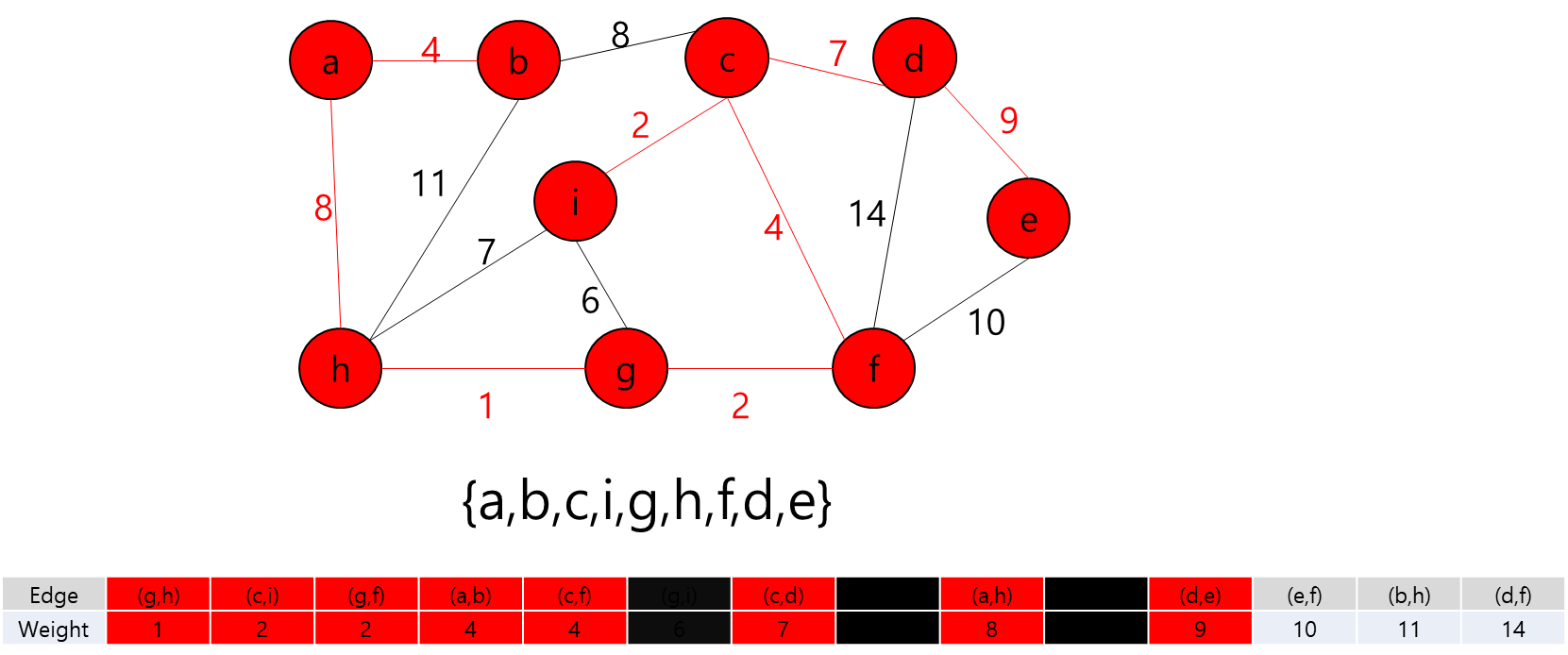
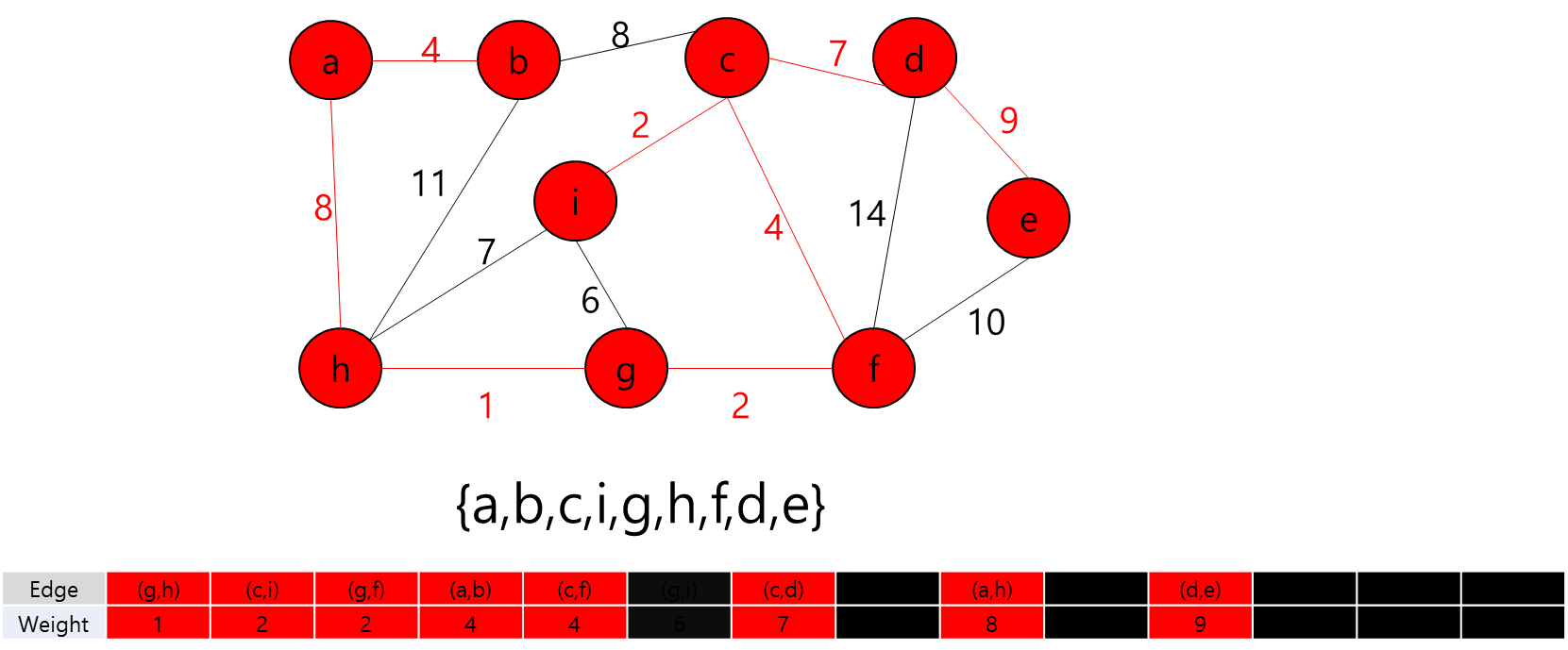
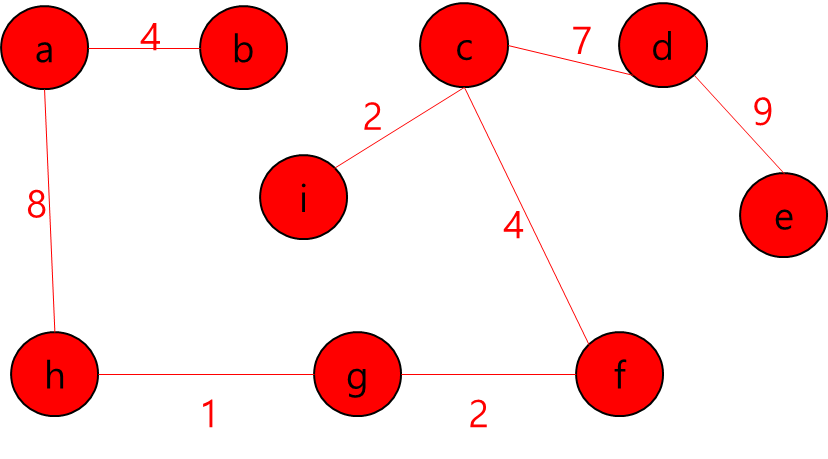
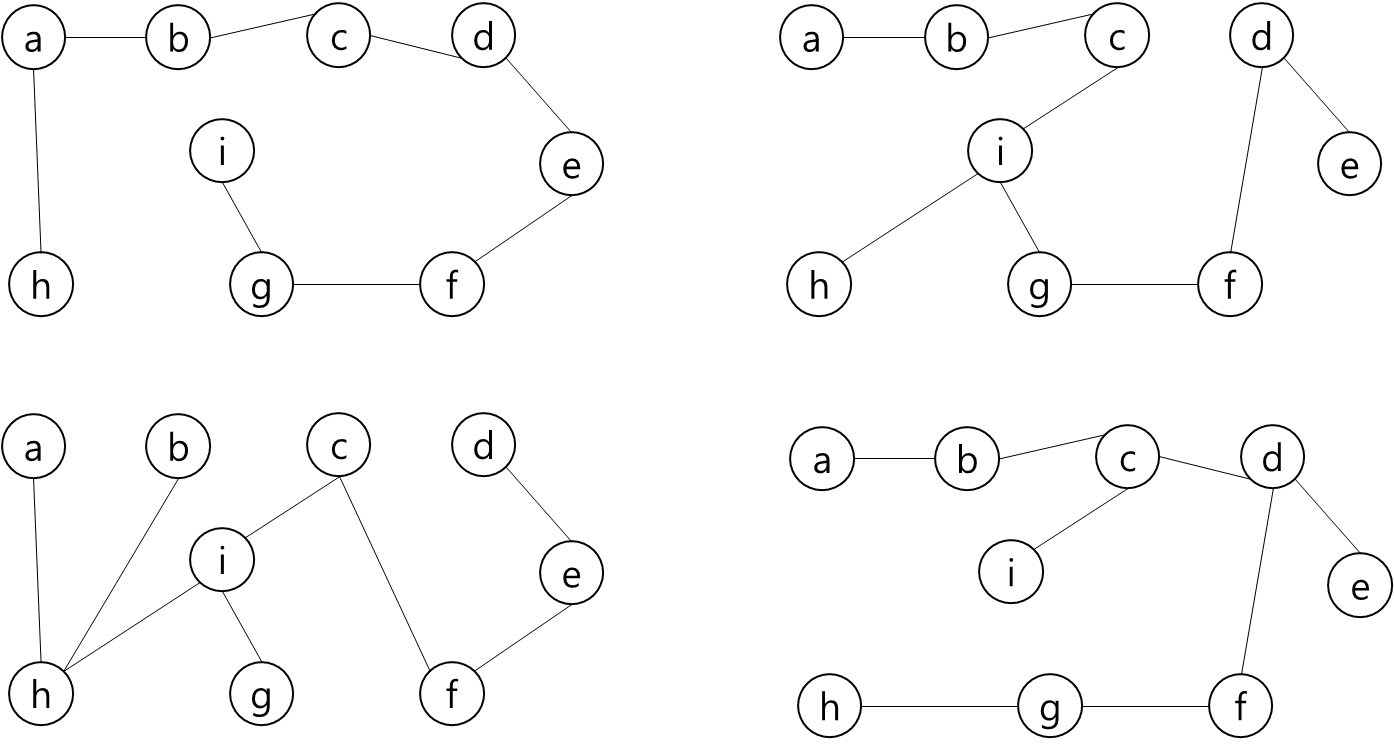
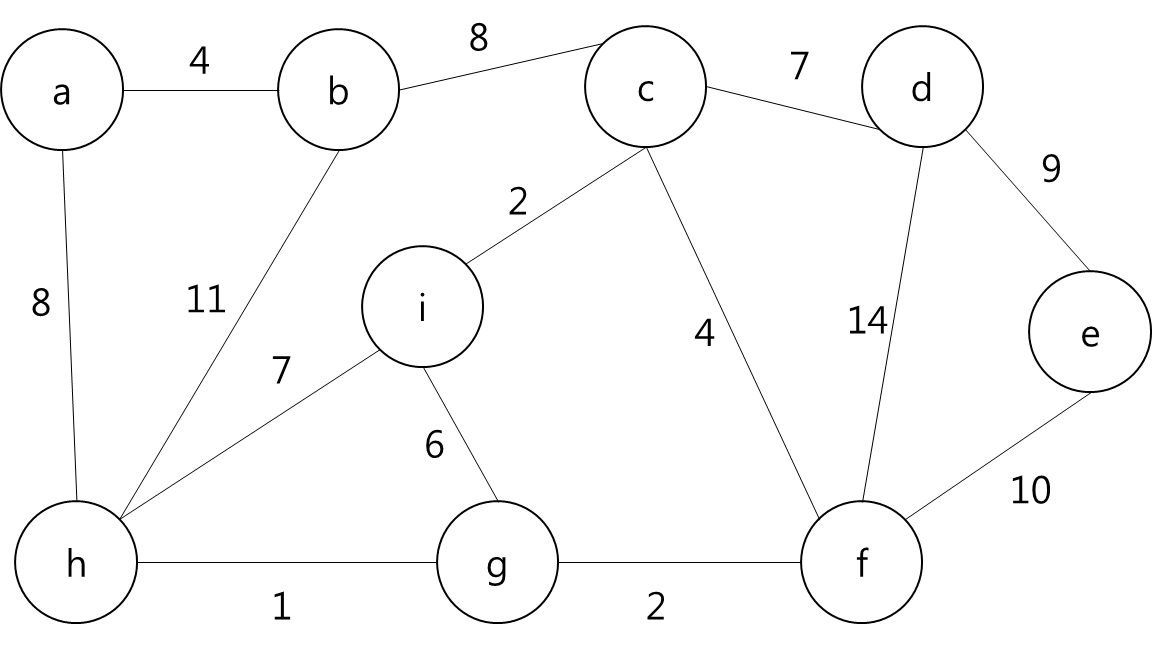
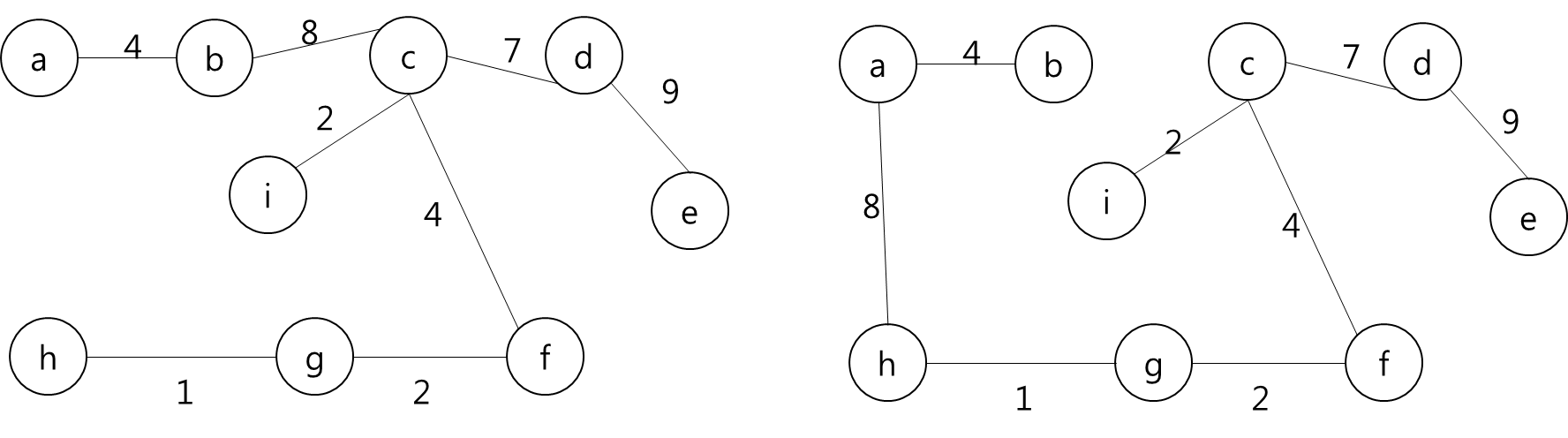
• 그렇다는 것은..? 각 지점을 정점이라고 가정하고 각 정점끼리 간선이 이어져 있고 이 간선들을 이용해서 최소 신장 트리를 만들라는 얘기가 될 것이다.
• 최소 신장 트리를 만들 수 없는 경우에는 -1을 출력하면 될 것이고, 최소 신장 트리가 만들어질 경우에는 그 가중치의 최솟값을 출력하면 되겠다.
• 그렇다면 정점은 입력으로 주어진 map의 좌표를 이용해서 저장하면 될 것이고... 각 정점간의 간선을 어떻게 만들것인가.. map에서 상하좌우로만 움직일 수 있고, 각 좌표간 거리는 1이라고 했으니까 BFS를 이용해서 각 정점간의 거리를 구하고 그것을 이용해서 간선을 구현하면 되겠다.

드가보자

3. 코드 (자바, 통과한 코드)

package baekjoon.mst.복제로봇_20220120;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Comparator;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;

public class Main {

  private static BufferedReader reader;
  private static int[] pointY = {0, 0, 1, -1};
  private static int[] pointX = {1, -1, 0, 0};
  private static List<int[]> edges;
  private static Vertex[] vertices;
  private static int[] parents;

  public static void main(String[] args) throws IOException {
    reader = new BufferedReader(new InputStreamReader(System.in));
    edges = new ArrayList<>();

    String[] parts = reader.readLine().split(" ");
    int mapSize = Integer.parseInt(parts[0]);
    int vertexCount = Integer.parseInt(parts[1]) + 1;
    vertices = new Vertex[vertexCount];
    char[][] maps = buildMapsAndAddVertex(mapSize);

    for (Vertex vertex : vertices) {
      getEdgesUsingBFS(maps, vertex);
    }

    parents = makeSet();
    int result = kruskal();

    System.out.println(isMST() ? result : -1);
  }

  private static char[][] buildMapsAndAddVertex(int mapSize) throws IOException {
    char[][] maps = new char[mapSize][mapSize];
    int vertexIndex = 0;

    for (int i = 0; i < mapSize; i++) {
      String line = reader.readLine();
      for (int j = 0; j < mapSize; j++) {
        maps[i][j] = line.charAt(j);
        if (isSourceOrKey(maps[i][j])) {
          vertices[vertexIndex] = new Vertex(i, j, vertexIndex++);
        }
      }
    }
    return maps;
  }

  private static boolean isSourceOrKey(char c) {
    return c == 'S' || c == 'K';
  }

  private static void getEdgesUsingBFS(char[][] maps, Vertex sourceVertex) {
    Queue<int[]> queue = new LinkedList<>();
    boolean[][] visit = new boolean[maps.length][maps.length];
    visit[sourceVertex.y][sourceVertex.x] = true;
    queue.add(new int[]{sourceVertex.y, sourceVertex.x, 0});

    while (!queue.isEmpty()) {
      int[] current = queue.poll();
      int currentY = current[0];
      int currentX = current[1];
      int distanceFromSourceVertex = current[2];

      for (int i = 0; i < 4; i++) {
        int nextY = currentY + pointY[i];
        int nextX = currentX + pointX[i];

        if (!visit[nextY][nextX] && isValidPoint(maps, nextY, nextX)) {
          visit[nextY][nextX] = true;
          queue.add(new int[]{nextY, nextX, distanceFromSourceVertex + 1});

          if (isSourceOrKey(maps[nextY][nextX])) {
            for (Vertex destinationVertex : vertices) {
              if (destinationVertex.y == nextY && destinationVertex.x == nextX) {
                edges.add(new int[]{sourceVertex.id, destinationVertex.id, distanceFromSourceVertex + 1});
                break;
              }
            }
          }
        }
      }
    }
  }

  private static boolean isValidPoint(char[][] maps, int nextY, int nextX) {
    return (nextY >= 0 && nextY < maps.length)
        && (nextX >= 0 && nextX < maps.length)
        && (maps[nextY][nextX] != '1');
  }

  private static int kruskal() {
    edges.sort(Comparator.comparingInt(x -> x[2]));
    int result = 0;
    for (int[] edge : edges) {
      int from = edge[0];
      int to = edge[1];
      int weight = edge[2];

      if (find(parents, from) != find(parents, to)) {
        union(parents, from, to);
        result += weight;
      }
    }
    return result;
  }

  private static int[] makeSet() {
    int[] parents = new int[vertices.length];
    for (int i = 0; i < parents.length; i++) {
      parents[i] = i;
    }
    return parents;
  }

  private static int find(int[] parents, int x) {
    if (parents[x] == x) {
      return x;
    }
    return parents[x] = find(parents, parents[x]);
  }

  private static void union(int[] parents, int x, int y) {
    x = find(parents, x);
    y = find(parents, y);

    if (x == y) {
      return;
    }

    if (x < y) {
      parents[y] = x;
    } else {
      parents[x] = y;
    }
  }

  private static boolean isMST() {
    for (int i = 0; i < vertices.length; i++) {
      if (find(parents, i) != 0) {
        return false;
      }
    }
    return true;
  }

  private static class Vertex {

    int y;
    int x;
    int id;

    public Vertex(int y, int x, int id) {
      this.y = y;
      this.x = x;
      this.id = id;
    }
  }
}

부가 설명 없이 코드만 보고 이해할 수 있는 코드...라고 믿고 부가 설명은 달지 않는다. (이해가 안되신다면 댓글 감사하겠습니다..)

근데 틀렸었다.

틀린 이유를 코드를 보면서 골똘히 생각해봤는데 두 부분에서 버그가 있었다.

          if (isSourceOrKey(maps[nextY][nextX])) {
            for (Vertex destinationVertex : vertices) {
              int destinationVertexId = -1;
              if (destinationVertex.y == nextY && destinationVertex.x == nextX) {
                destinationVertexId = destinationVertex.id;
                break;
              }
              edges.add(
                  new int[]{sourceVertex.id, destinationVertex.id, distanceFromSourceVertex + 1});
            }
          }

BFS를 이용해서 각 Vertex간의 거리를 구하고 탐색하는 좌표가 Vertex에 해당하면 Edge를 만들어 저장하는 부분이다. 여기서 edges.add() 부분이 if (destinationVertex.y == nextY && destinationVertex.x == nextX) 안에 있어야 했다. 그렇지 않으면 index가 -1인 상태로 edges에 추가되어서 버그가 발생할 수 있다.

    parents = makeSet();
    int result = kruskal();

    System.out.println(!edges.isEmpty() ? result : -1);

모든 Key에 닿을 수 있는 경우 가중치의 최솟값을 출력하고 그렇지 않은 경우 -1을 리턴하는 부분이다. 여기서 edges가 비어있는 경우를 모든 Key에 닿을 수 없는 경우로 생각하고 작성했는데, 생각해보니 edges 있어도 모든 Key에 닿을 수 있는 경우가 있을 수 있다. 그래서 find() 메소드로 모든 vertex들이 같은 집합인지 체크하는 isMST() 메소드를 작성하여 수정했다. 

Prim(프림) 알고리즘

그래프의 모든 정점을 최소 비용으로 연결하는, 즉, 최소 신장 트리를 구현하는 대표적인 Greedy(탐욕) 알고리즘이다.

Greedy 알고리즘

• 그 순간에 가장 좋다고 생각되는 해를 선택
  • MST에 포함된 정점들과 그렇지 않은 정점들을 잇는 간선중 가장 가중치가 작은 간선을 선택하여 MST에 추가
• 그 순간에는 최적의 해일 수 있지만, 전체적으로 봤을때는 그렇지 않을 수 있으므로 반드시 검증을 해야함
  • 정점이 이미 선택되어 MST에 포함되어 있는지 검증
• Kruskal(크루스칼) 알고리즘의 경우는 간선을 선택하는 Greedy 알고리즘이다.

동작방식

1. 임의의 정점을 출발 정점으로 선택
2. 매 단계에서 이전단계에 MST에 포함된 정점들과 포함되지 않은 정점들을 잇는 간선 중 가중치가 가장 작은 간선을 선택하여 MST를 확장한다.
3. 간선개수가 \(N-1\)이 될 때까지 반복(\(N\): 정잠개수)

Visualize

임의의 정점 a를 선택한다.

MST에 포함된 정점들(a)과 그렇지 않은 정점들을 잇는 간선들 중에 가중치가 가장 작은 간선 (a,b)를 MST에 추가 

MST에 포함된 정점들(a,b)과 그렇지 않은 정점들을 잇는 간선 중 가중치가 가장 작은 간선((a,h))를 MST에 추가

MST에 포함된 정점들(a,b,h)과 그렇지 않은 정점들을 잇는 간선 중 가중치가 가장 작은 간선((h,g))를 MST에 추가

MST에 포함된 정점들(a,b,h,g)과 그렇지 않은 정점들을 잇는 간선 중 가중치가 가장 작은 간선((g,f))를 MST에 추가

MST에 포함된 정점들(a,b,h,g,f)과 그렇지 않은 정점들을 잇는 간선 중 가중치가 가장 작은 간선((c,f))를 MST에 추가

MST에 포함된 정점들(a,b,h,g,f,c)과 그렇지 않은 정점들을 잇는 간선 중 가중치가 가장 작은 간선((c,i))를 MST에 추가

MST에 포함된 정점들(a,b,h,g,f,c,i)과 그렇지 않은 정점들을 잇는 간선 중 가중치가 가장 작은 간선((d,e))를 MST에 추가

모든 정점들이 MST에 포함되어 있고 간선의 개수가 정점 개수 - 1 이므로 끝

시간 복잡도

간선의 가중치가 최소인 간선 탐색: \(O(n)\)

MST에 포함된 정점과 그렇지 않은 정점들 사이의 거리 갱신: \(O(n)\)

이것을 정점의 수 만큼 반복하므로 \((O(n) + O(n)) * (n-1) = O(n^2)\)

그러나 우선순위 큐(Priority Queue)를 사용하는 경우에는 \(O(nlgn)\)이다.

코드

class MSTPrim {
  int[][] graph;
  
  public MSTPrim() {
    this.graph = {
      {0, 4, 0, 0, 0, 0, 0, 8, 0},
      {4, 0, 8, 0, 0, 0, 0, 11, 0},
      {0, 8, 0, 7, 0, 4, 0, 0, 7},
      {0, 0, 7, 0, 9, 14, 0, 0, 0},
      {0, 0, 0, 9, 10, 0, 0, 0, 0},
      {0, 0, 4, 14, 10, 0, 2, 0, 0},
      {0, 0, 0, 0, 0, 2, 0, 1, 7},
      {8, 11, 0, 0, 0, 0, 1, 0, 7},
      {0, 0, 2, 0, 0, 0, 6, 7, 0},
    };
  }
  
  public int prim(startVertex) {
    int vertexCount = graph.length;
    int[] distance = new int[vertexCount];
    boolean[] visit = new boolean[vertexCount];
    Arrays.fill(distance, Integer.MAX_VALUE);
    
    int result = 0;
    distance[startVertex] = 0;
    
    for(int i = 0; i < vertexCount; i++) {
      int minDistanceFromMst = Integer.MAX_VALUE;
      int targetVertex = -1;
      for(int j = 0; j < vertexCount; j++) {
        if(!visit[j] && distance[j] < minDistanceFromMst) {
          minDistanceFromMst = distance[j];
          targetVertex = j;
        }
      }
      
      visit[targetVertex] = true;
      result += minDistanceFromMst;
      
      for(int j = 0; j < vertexCount; j++) {
        if(!visit[j] && graph[targetVertex][j] > 0 && graph[targetVertex][j] < distance[j]) {
          distance[j] = graph[targetVertex][j];
        }
      }
    }
    
    return result; 
  }
  
  public int prim_using_priority_queue(startVertex) {
    int vertexCount = graph.length;
    boolean[] visit = new boolean[vertexCount];
    // int[] -> {destination, weight}
    PriorityQueue<int[]> queue = new PriorityQueue<>(Comparator.comparingInt(x -> x[1]);
    
    queue.add(new int[]{startVertex, 0})
    int result = 0;
    
    while(!queue.isEmpty()) {
      int[] current = queue.poll();
      int destination = current[0];
      int weight = current[1];
      if(visit[destination]) {
        continue;
      }
      
      visit[destination] = true;
      result += weight;
      
      for(int i = 0; i < vertexCount; i++) {
        if(!visit[i] && graph[destination][i] > 0) {
          queue.add(new int[]{i, graph[destination][i]};
        }
      }
    }
    
    return result; 
  }
}

같이 볼 자료

2022.01.16 - [Algorithm] - [Algorithm] MST (Minimum Spanning Tree, 최소 신장 트리)

2022.01.16 - [Algorithm] - [Algorithm] Krsukal (크루스칼) 알고리즘

Kruskal (크루스칼) 알고리즘

그래프의 모든 정점을 최소 비용으로 연결하는, 즉, 최소 신장 트리를 구현하는 대표적인 Greedy(탐욕) 알고리즘이다.

Greedy 알고리즘

• 그 순간에 가장 좋다고 생각되는 해를 선택
  • 정렬 된 간선 중 가중치가 가장 작은 간선부터 차례대로 선택
• 그 순간에는 최적의 해일 수 있지만, 전체적으로 봤을때는 그렇지 않을 수 있으므로 반드시 검증을 해야함
  • 이미 선택된 간선인지, 사이클을 형성하는지 검증
• Prim(프림) 알고리즘의 경우는 정점을 선택하는 Greedy 알고리즘이다.

동작방식

1. 그래프의 간선들을 오름차순으로 정렬한다.
2. 정렬된 간선들을 차례대로 선택한다.
3. 단, 이미 선택된 간선과 사이클을 형성하는 간선은 패스
4. 간선의 개수가 \(N-1\)개가 될 때까지 반복한다 (\(N\): 정점 개수)

Visualize

처음은 어떠한 정점들도 선택되지 않은 상태, 간선들을 오름차순 정렬

정렬된 간선을 차례대로 선택하여 MST에 추가한다. 간선 (g,h)를 추가하고 정점 g,h를 같은 집합으로 합친다.

간선 (c,i)를 추가하고 정점 c와 i를 같은 집합으로 합친다.

간선 (g,f)를 추가하고 정점 f와 g를 같은 집합으로 합친다.

간선 (a,b)를 추가하고 정점 a와 b를 같은 집합으로 합친다.

간선 (c,f)를 추가하고 정점 c와 f를 같은 집합으로 합친다.

간선 (g,i)를 추가하려고 하는데.. 정점 g와 i는 이미 같은 집합이다. 만약 간선 (g,i)를 추가하면 사이클이 형성된다. 그러므로 그냥 패스

간선 (c,d)를 추가하고 정점 c와 d를 같은 집합으로 합친다.

간선 (h,i)를 추가하려고 하는데.. 정점 h와 i는 이미 같은 집합이다. 만약 간선 (h,i)를 추가하면 사이클이 형성된다. 그러므로 그냥 패스

간선 (a,h)를 추가하고 a와 h를 같은 집합으로 합친다.

간선 (b,c)를 추가하려고 하는데... b와 c는 이미 같은 집합이다. 만약 간선 (b,c)를 추가한다면 사이클이 형성된다. 그러므로 그냥 패스

간선 (d,e)를 추가하고 정점 d와 e를 같은 집합으로 합친다.

모든 정점들이 같은 집합이고, MST에 추가된 간선이 정점 개수 - 1이므로 끝

사이클을 형성하는 지 검증할 때 Union-Find 알고리즘을 사용한다

시간복잡도

Union-Find 알고리즘을 사용하면 간선들을 정렬하는 시간에 영향받는다.

즉, 간선 \(E\)개를 Quick Sort의 효율로 정렬한다면 \(O(ElogE)\)이다.

코드

class MSTKruskal {
  int[] parents;
  int[][] graph;
  
  public MSTKruskal() {
    this.graph = {
      {0, 4, 0, 0, 0, 0, 0, 8, 0},
      {4, 0, 8, 0, 0, 0, 0, 11, 0},
      {0, 8, 0, 7, 0, 4, 0, 0, 7},
      {0, 0, 7, 0, 9, 14, 0, 0, 0},
      {0, 0, 0, 9, 10, 0, 0, 0, 0},
      {0, 0, 4, 14, 10, 0, 2, 0, 0},
      {0, 0, 0, 0, 0, 2, 0, 1, 7},
      {8, 11, 0, 0, 0, 0, 1, 0, 7},
      {0, 0, 2, 0, 0, 0, 6, 7, 0},
    }
  }
  
  public int kruskal() {
    int[][] edges = buildEdges();
    makeSet();
    int result = 0;
    
    for(int i = 0; i < edges.lengh; i++) {
      int source = edges[i][0];
      int destination = edges[i][1];
      int weight = edges[i][2];
      
      if(find(source) != find(destination)) {
        union(source, destination);
        result += weight;
      }
    }
    
    return result;
  }
  
  public int[][] buildEdges() {
    int[][] edges = new int[][]{};
    index = 0;
    
    for(int i = 0; i < graph.length; i++) {
      for(int j = 0; j < graph.length; j++) {
        if(graph[i][j] !=0) {
          edges[index++] = {i, j, graph[i][j]};
          edges[index++] = {j, i, graph[j][i]};
        }
      }
    }
    
    return edges;
  }
  
  public void makeSet() {
    this.parents = new int[graph.length];
    
    for(int i = 0; i < graph.lenght; i++) {
      parents[i] = i;
    }
  }
  
  public int find(x) {
    if(parents[x] == x) {
      return x;
    }
    
    return parents[x] = find(parents[x]);
  }
  
  public int union(x, y) {
    x = find(x);
    y = find(y);
    
    if(x == y) {
      return;
    }
    
    if(x > y) {
      parents[y] = x;
    } else {
      parents[x] = y;
    }
    
  }
}

같이 볼 자료

2022.01.16 - [Algorithm] - [Algorithm] MST (Minimum Spanning Tree, 최소 신장 트리)

2022.01.16 - [Algorithm] - [Algorithm] Prim(프림) 알고리즘

신장 트리 (Spanning Tree)

• 그래프의 모든 정점을 연결하는 트리
• 트리: 일반적으로 계층구조의 자료구조를 생각하는데, 그래프 이론에서 사이클이 없는 무방향 그래프를 트리라고 한다.
• 그래프가 n개의 정점을 가질 때, 그래프의 최소 간선의 수는 n-1개이다.
• 하나의 그래프에서 여러개의 신장 트리가 존재할 수 있다.

최소 신장 트리 (Minimum Spanning Tree)

• Spanning Tree 중에서 사용된 간선들의 가중치 합이 최소인 트리
• Spanning Tree와 마찬가지로 정점이 N개일 때, N-1개의 간선으로 연결된다.
• Spanning Tree와 마찬가지로 사이클이 없다.
• Spanning Tree와 마찬가지로 MST의 해가 여러개 일 수 있다.

MST을 구현하는 알고리즘으로 Kruskal(크루스칼) 알고리즘과 Prim(프림) 알고리즘이 있다.

2022.01.16 - [Algorithm] - [Algorithm] Krsukal (크루스칼) 알고리즘

2022.01.16 - [Algorithm] - [Algorithm] Prim(프림) 알고리즘

1. 문제

https://www.acmicpc.net/problem/16398

문제 설명

홍익 제국의 중심은 행성 T이다. 제국의 황제 윤석이는 행성 T에서 제국을 효과적으로 통치하기 위해서, N개의 행성 간에 플로우를 설치하려고 한다.

두 행성 간에 플로우를 설치하면 제국의 함선과 무역선들은 한 행성에서 다른 행성으로 무시할 수 있을 만큼 짧은 시간만에 이동할 수 있다. 하지만, 치안을 유지하기 위해서 플로우 내에 제국군을 주둔시켜야 한다.

모든 행성 간에 플로우를 설치하고 플로우 내에 제국군을 주둔하면, 제국의 제정이 악화되기 때문에 황제 윤석이는 제국의 모든 행성을 연결하면서 플로우 관리 비용을 최소한으로 하려 한다.

N개의 행성은 정수 1,…,N으로 표시하고, 행성 i와 행성 j사이의 플로우 관리비용은 Cij이며, i = j인 경우 항상 0이다.

제국의 참모인 당신은 제국의 황제 윤석이를 도와 제국 내 모든 행성을 연결하고, 그 유지비용을 최소화하자. 이때 플로우의 설치비용은 무시하기로 한다.

제한 사항

입력

입력으로 첫 줄에 행성의 수 N (1 ≤ N ≤ 1000)이 주어진다.

두 번째 줄부터 N+1줄까지 각 행성간의 플로우 관리 비용이 N x N 행렬 (Cij), (1 ≤ i, j ≤ N, 1 ≤ Cij ≤ 100,000,000, Cij = Cji) 로 주어진다.

출력

모든 행성을 연결했을 때, 최소 플로우의 관리비용을 출력한다.

입출력 예

2. 어떻게 풀까?

• 최소 신장 트리이므로 Kruskal 알고리즘 혹은 Prim 알고리즘으로 해결한다.

3. 코드

Kruskal 알고리즘

import java.io.*;
import java.util.*;

 class Main {

  private static final BufferedReader READER = new BufferedReader(new InputStreamReader(System.in));
  private static final BufferedWriter WRITER = new BufferedWriter(new OutputStreamWriter(System.out));
  private static StringTokenizer tokenizer;
  private static int[] parents;

  public static void main(String[] args) throws IOException {
    tokenizer = new StringTokenizer(READER.readLine());
    int vertexCount = Integer.parseInt(tokenizer.nextToken());

    kruskal(vertexCount);

    WRITER.flush();
    WRITER.close();
    READER.close();
  }

  private static void kruskal(int vertexCount) throws IOException {
    List<int[]> edges = new ArrayList<>();
    for (int i = 1; i <= vertexCount; i++) {
      tokenizer = new StringTokenizer(READER.readLine());
      for (int j = 1; j <= vertexCount; j++) {
        int weight = Integer.parseInt(tokenizer.nextToken());
        if (weight != 0) {
          edges.add(new int[]{i, j, weight});
        }
      }
    }

    edges.sort(Comparator.comparingInt(o -> o[2]));

    parents = new int[vertexCount + 1];
    for (int i = 1; i <= vertexCount; i++) {
      parents[i] = i;
    }

    long sumWeight = 0;
    for (int i = 0; i < edges.size(); i++) {
      int[] current = edges.get(i);
      int from = current[0];
      int to = current[1];
      int weight = current[2];
      if (find(from) != find(to)) {
        union(from, to);
        sumWeight += weight;
      }
    }

    WRITER.write(sumWeight + "");
  }

  private static void union(int from, int to) {
    from = find(from);
    to = find(to);

    if (from > to) {
      parents[to] = from;
    } else {
      parents[from] = to;
    }
  }

  private static int find(int x) {
    if (parents[x] == x) {
      return x;
    }
    return parents[x] = find(parents[x]);
  }
}

Prim 알고리즘

import java.io.*;
import java.util.*;

 class Main {

  private static final BufferedReader READER = new BufferedReader(new InputStreamReader(System.in));
  private static final BufferedWriter WRITER = new BufferedWriter(new OutputStreamWriter(System.out));
  private static StringTokenizer tokenizer;

  public static void main(String[] args) throws IOException {
    tokenizer = new StringTokenizer(READER.readLine());
    int vertexCount = Integer.parseInt(tokenizer.nextToken());

    prim(vertexCount);

    WRITER.flush();
    WRITER.close();
    READER.close();
  }

  private static void prim(int vertexCount) throws IOException {
    int[][] adjMatrix = new int[vertexCount + 1][vertexCount + 1];
    for (int i = 1; i <= vertexCount; i++) {
      tokenizer = new StringTokenizer(READER.readLine());
      for (int j = 1; j <= vertexCount; j++) {
        adjMatrix[i][j] = Integer.parseInt(tokenizer.nextToken());
      }
    }

    PriorityQueue<int[]> queue = new PriorityQueue<>(Comparator.comparingInt(o -> o[1]));
    boolean[] visit = new boolean[vertexCount + 1];
    queue.add(new int[]{1, 0});

    long sumWeight = 0;
    while (!queue.isEmpty()) {
      int[] current = queue.poll();
      int to = current[0];
      int weight = current[1];

      if (visit[to]) {
        continue;
      }
      visit[to] = true;
      sumWeight += weight;

      for (int i = 1; i <= vertexCount; i++) {
        if (adjMatrix[to][i] != 0) {
          queue.add(new int[]{i, adjMatrix[to][i]});
        }
      }
    }

    WRITER.write(sumWeight + "");
  }
}

4. 느낀 점

• 최소 신장 트리의 Prim, Kruskal 알고리즘을 안다면 쉽게 풀 수 있는 문제