Dev 일기장

1. 문제

https://programmers.co.kr/learn/courses/30/lessons/43163

문제 설명

제한 사항

입출력 예

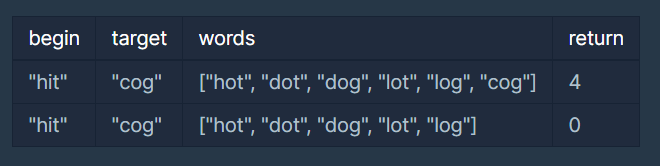
2. 어떻게 풀까?

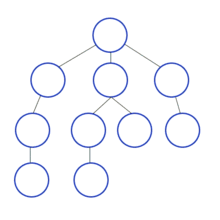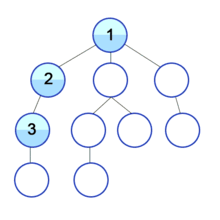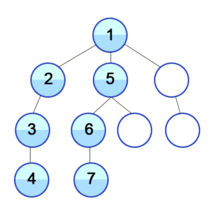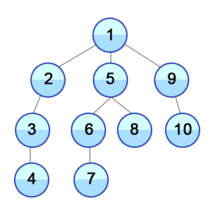
• 인자로 주어지는 begin에서 시작해서 words에 주어진 단어들과 비교하면서 알파벳 하나만 바꿔서 그 단어가 될 수 있는지 확인한다.
• words내에 방문한 단어들을 방문 표시하고, 모든 단어들을 방문하거나 target과 같은 단어를 방문하고 난 뒤에는 다시 방문 표시를 지워주어야 한다. 이게 무슨소리냐.. 말로 설명하니 어려우니까 그림으로 대체

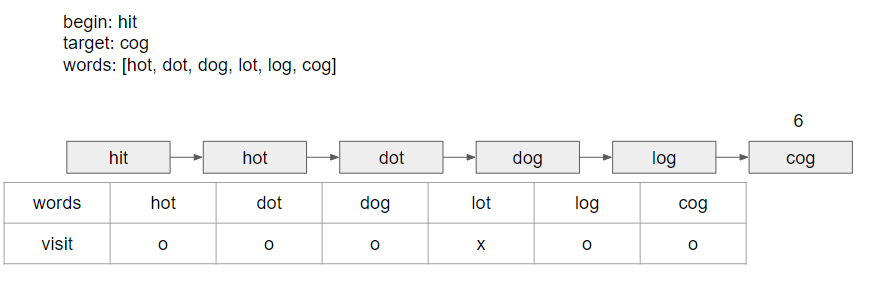
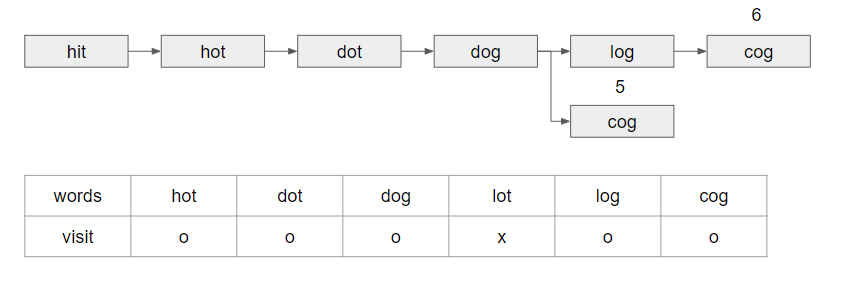
• 아니 그럼 visit을 굳이 둘 필요 없지않냐? 라고 생각할 수도 있는데.... 그러면 무한루프에 hot → dot → hot → dot ... 이런식으로 무한루프에 빠지니까 visit또한 반드시 필요하다.

• hit에서 hot으로, hot에서 dog로 알파벳 하나를 바꿔서 만들 수 있는 단어라는 것을 우리는 직관적으로 알 수 있지만 이것을 코드로는 어떻게 구현할까?
• 단어와 단어 한 글자씩 비교하면서 다른 글자라면 count를 증가시키고, 그 count가 1이라면 알파벳 하나를 바꿔 만들 수 있는 단어가 된다고 판단하면 되겠다.

3. 코드 (Java)

package programmers.level3.단어변환_20220125;

import java.util.HashMap;
import java.util.Map;

public class Solution {

  public int result = Integer.MAX_VALUE;
  public Map<String, Boolean> visit;

  public int solution(String begin, String target, String[] words) {
    visit = new HashMap<>();
    for (String word : words) {
      visit.put(word, false);
    }
    dfs(begin, target, words, 0);
    return result == Integer.MAX_VALUE ? 0 : result;
  }

  private void dfs(String currentWord, String targetWord, String[] words, int distance) {

    if (currentWord.equals(targetWord)) {
      result = Math.min(result, distance);
      return;
    }

    for (String word : words) {
      if (!visit.get(word) && getCharDifferenceCount(currentWord, word) == 1) {
        visit.replace(word, true);
        dfs(word, targetWord, words, distance + 1);
        visit.replace(word, false);
      }
    }
  }

  private int getCharDifferenceCount(String a, String b) {
    if (a.length() != b.length()) {
      return -1;
    }

    int result = 0;
    for (int i = 0; i < a.length(); i++) {
      if (a.charAt(i) != b.charAt(i)) {
        result++;
      }
    }
    return result;
  }
}

사실 틀렸었다.

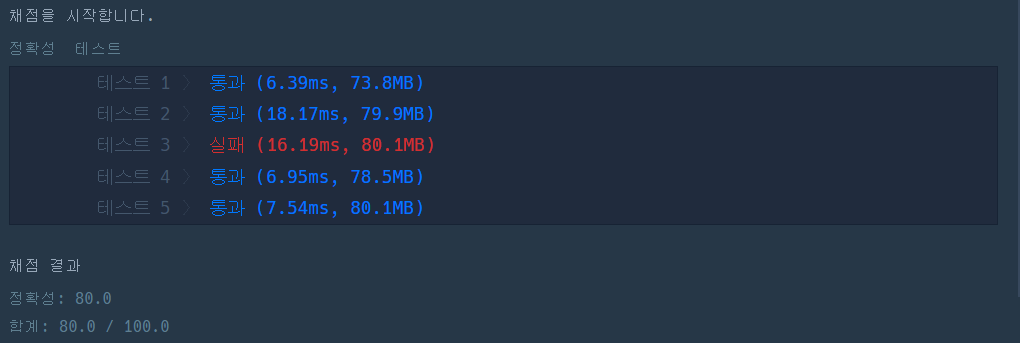
이유를 생각해봤는데.... 알파벳을 한 번 바꿔서 일치하는지 체크하는 부분에서 실수를 저질렀다.

    for (String word : words) {
      String erase = currentWord.replaceAll("[" + word + "]", "");
      if (!visit.get(word) && erase.length() == 1) {
        visit.replace(word, true);
        dfs(word, targetWord, words, distance + 1);
        visit.replace(word, false);
      }
    }

내 생각은 이랬다. "hot"에서 정규표현식을 이용하여 "[hit]"에 매치되는 부분을 지우면 "o"만 남게되고 그러면 알파벳 차이가 1개이니까 조건에 부합하겠구나! 나 천잰듯?

천재가 아니라 멍청이었다.

만약 단어가 "hto"였다면 어떨까? "hto" → "hit"가 되려면 알파벳을 2개 바꿔야한다. (t → i, o → t) 근데 저 코드대로라면 erase는 역시 "o"만 남게되고 조건에 맞으니까 if문을 통과하게 된다.

아니.. 개 허술한 코드였는데.. 다 틀려야지 하나만 틀리니까 더 찾기 힘들잖아.....................

그래서 정공법으로 코드 수정한 결과가 getCharDifferenceCount() 메소드를 이용한 것이었다.

그나마 다행인 것은 구글링해서 뭐가 틀렸는지 확인한 것이 아니라 스스로 틀린 부분을 생각해낸 부분이라는점..?

그래프 순회

• 그래프에서 임의의 한 정점에서 출발하여 모든 정점을 한번씩 방문하는 작업
• 탐색하는 동안 이미 방문한 정점이 있을 수 있으므로 방문했다는 표시를하여 중복방문을 피한다.
• 대표적으로 DFS와 BFS가 있다.

DFS (Depth-First-Search): 깊이 우선 탐색

• 출발노드에서 하위노드(자식노드)를 먼저 탐색하는 방식
• 일반적으로 Stack이나 Recursive를 이용하여 구현한다.

동작방식

1. 시작노드에서 간선을 따라 다음노드로 방문한다.
2. 더이상 탐색할 간선이 없다면 역추적(Backtracking)을 통해 이전노드로 이동하여 아직 탐색하지 않은 간선을 참색한다.
3. 모든 노드를 탐색할 때까지 반복한다.

Visualize

E노드에서 더이상 이동 할 간선이 없으므로 역추적으로 통해 B노드로 이동, B노드에서도 마찬가지로 더이상 이동할 간선이 없으므로 A노드로 이동 후 다음 간선인 (A,C)을 통해 C노드로 이동

F노드에서 더이상 이동할 간선이 없으므로 역추적을 통해 C노드로 이동, C노드에서 다음 간선인 (C,G)을 통해 G노드로 이동

I노드에서 더이상 이동할 간선이 없으므로 역추적을 통해 G노드로 이동, G노드에서도 마찬가지로 C노드로 이동, C노드에서도 마찬가지로 A노드로 이동, A노드에서 다음 간선인 (A,D)를 통해 D노드로 이동

코드

의사코드

DFS(graph, current_node, visit) {
  visit[current_node] = true
  
  for( adjacent_node to current_node) {
    if(!visit[adjacent_node]) {
      DFS(graph, adjacent_node, visit)
    }
  }
}

코드 - Recursive (Java)

class DFS_Recursive {

  private int[][] graph;
  
  private boolean[] visit;
  
  public DFS_Recursive() {
    this.graph = {
      {0, 1, 1, 1, 0, 0, 0, 0, 0},
      {1, 0, 0, 0, 1, 0, 0, 0, 0},
      {1, 0, 0, 0, 0, 1, 1, 0, 0},
      {1, 0, 0, 0, 0, 0, 0, 1, 0},
      {0, 1, 0, 0, 0, 0, 0, 0, 0},
      {0, 0, 1, 0, 0, 0, 0, 0, 1},
      {0, 0, 1, 0, 0, 0, 0, 0, 0},
      {0, 0, 0, 1, 0, 0, 0, 0, 0},
      {0, 0, 0, 0, 0, 1, 0, 0, 0},
    };
    visit = new boolean[graph.length];
  }
  
  public void dfs(currentNode) {
    visit[currentNode] = true;
    
    for(int i = 0; i < graph[currentNode].length; i++) {
      if(isAdjacentNode(currentNode, i) && !visit[i]) {
        dfs(i);
      }
    }
  }
  
  public boolean isAdjacentNode(int currentNode, int targetNode) {
    return graph[currentNode][targetNode] == 1;
  }

}

코드 - Stack

class DFS_Stack {

  private int[][] graph;
  
  private boolean[] visit;
  
  public DFS_Stack() {
    this.graph = {
      {0, 1, 1, 1, 0, 0, 0, 0, 0},
      {1, 0, 0, 0, 1, 0, 0, 0, 0},
      {1, 0, 0, 0, 0, 1, 1, 0, 0},
      {1, 0, 0, 0, 0, 0, 0, 1, 0},
      {0, 1, 0, 0, 0, 0, 0, 0, 0},
      {0, 0, 1, 0, 0, 0, 0, 0, 1},
      {0, 0, 1, 0, 0, 0, 0, 0, 0},
      {0, 0, 0, 1, 0, 0, 0, 0, 0},
      {0, 0, 0, 0, 0, 1, 0, 0, 0},
    };
    visit = new boolean[graph.length];
  }
  
  public void dfs(startNode) {
    Stack<Integer> stack = new Stack();
    
    stack.push(startNode);
    visit[startNode] = true;
    
    while(!stack.isEmpty()) {
      int currentNode = stack.pop();
      
      for(int i = 0; i < graph[currentNode].length; i++) {
        if(isAdjacentNode(i) && !visit[i]) {
          stack.push(i);
          visit[i] = true;
        }
      }
    }
  }
  
  public boolean isAdjacentNode(int currentNode, int targetNode) {
    return graph[currentNode][targetNode] == 1;
  }

}

시간복잡도

• 인접 리스트: \(O(N+E)\) (\(N\): 정점 개수, \(E\): 간선 개수)
• 인접 행렬: \(O(N^2)\)

참고

2021.04.14 - [Algorithm] - [Algorithm] 그래프 (Graph)

2022.01.08 - [Algorithm] - [Algorithm] BFS (Breath-First-Search, 너비 우선 탐색)