# 개요
다익스트라 알고리즘 정리
용어가 좀 혼용 될 수 있다.
- Ex) 노드 == 정점, 엣지 == 간선
# Dijkstra (다익스트라) 알고리즘
- 음수 가중치가 없는 그래프에서 한 정점에서 다른 모든 정점까지의 최단 경로 및 거리를 구하는 알고리즘
- Bellman Ford 알고리즘과의 차이
- 음수 가중치가 있다면 동작하지 않는다.
- O(n^2)로 Bellman Ford 알고리즘 보다 빠르다. (우선 순위 큐를 사용한다면 mlogn, m은 간선 개수)
# 동작 과정
그림으로 설명

노드 0부터 다른 모든 노드 까지의 최단 경로 거리를 구하려고 한다.
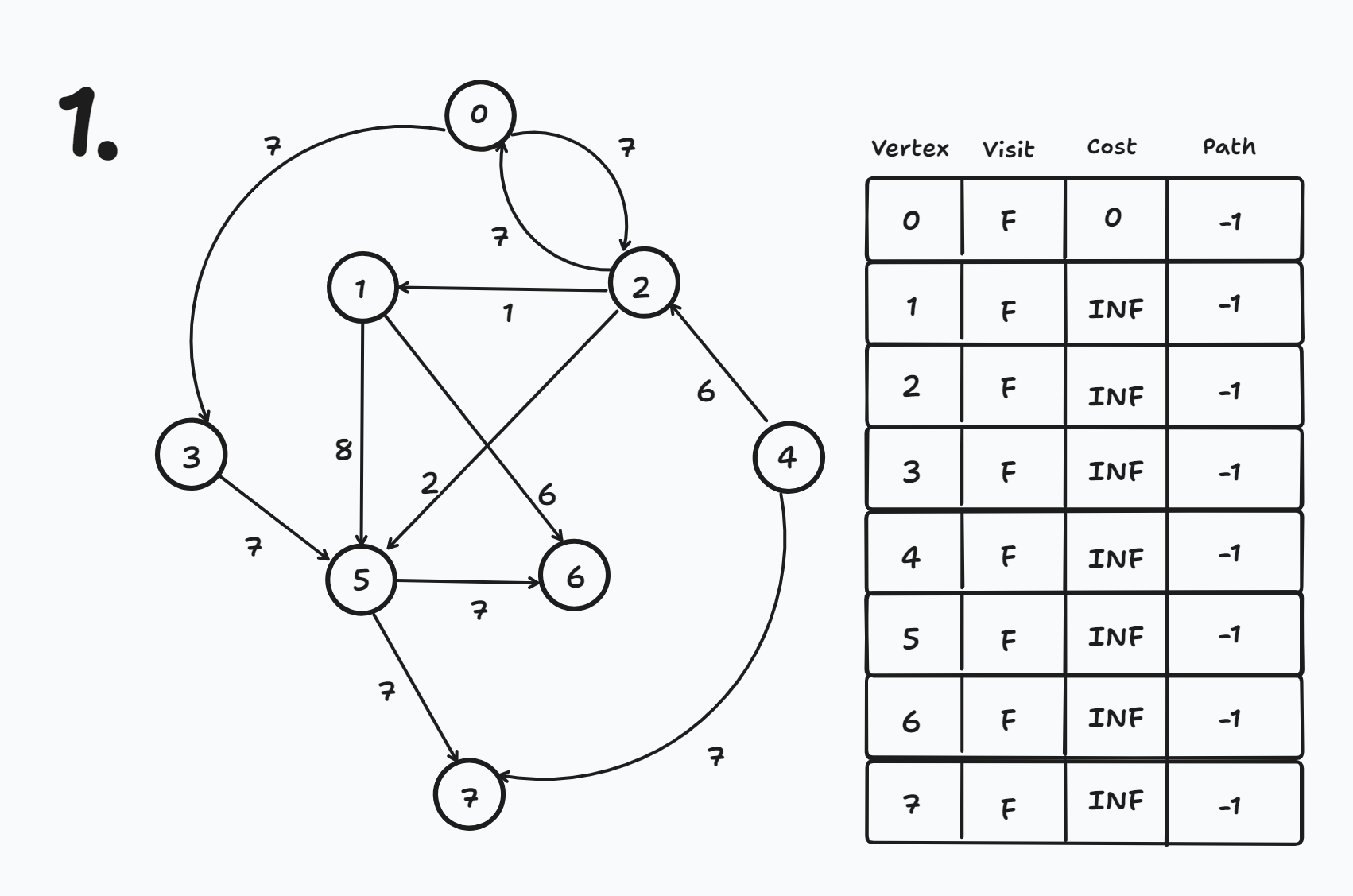
초기화, 출발 노드가 0번 노드이므로 cost[0] = 0으로 초기화한다.
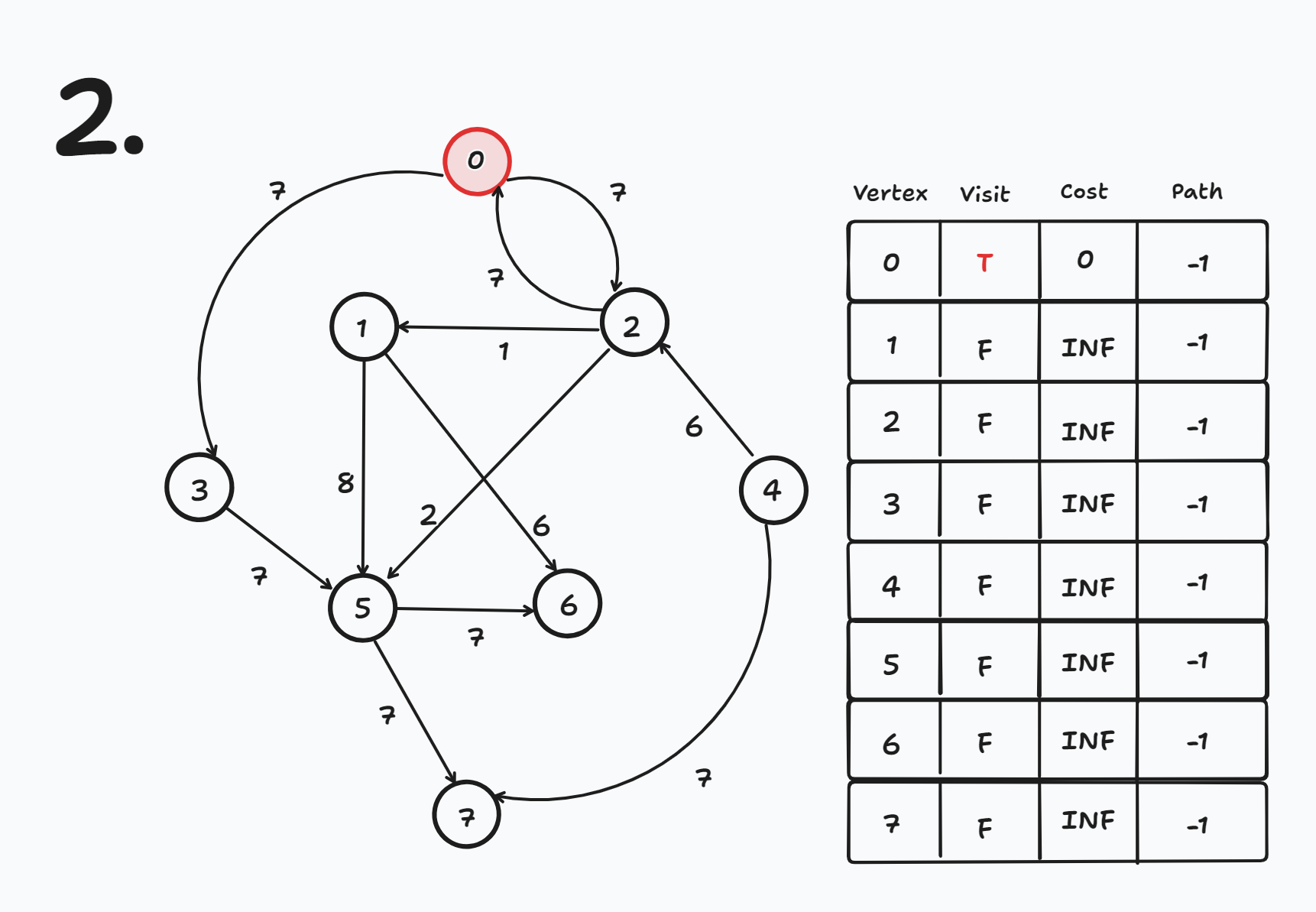
출발 노드인 0번 노드 방문
- visit[0] = true
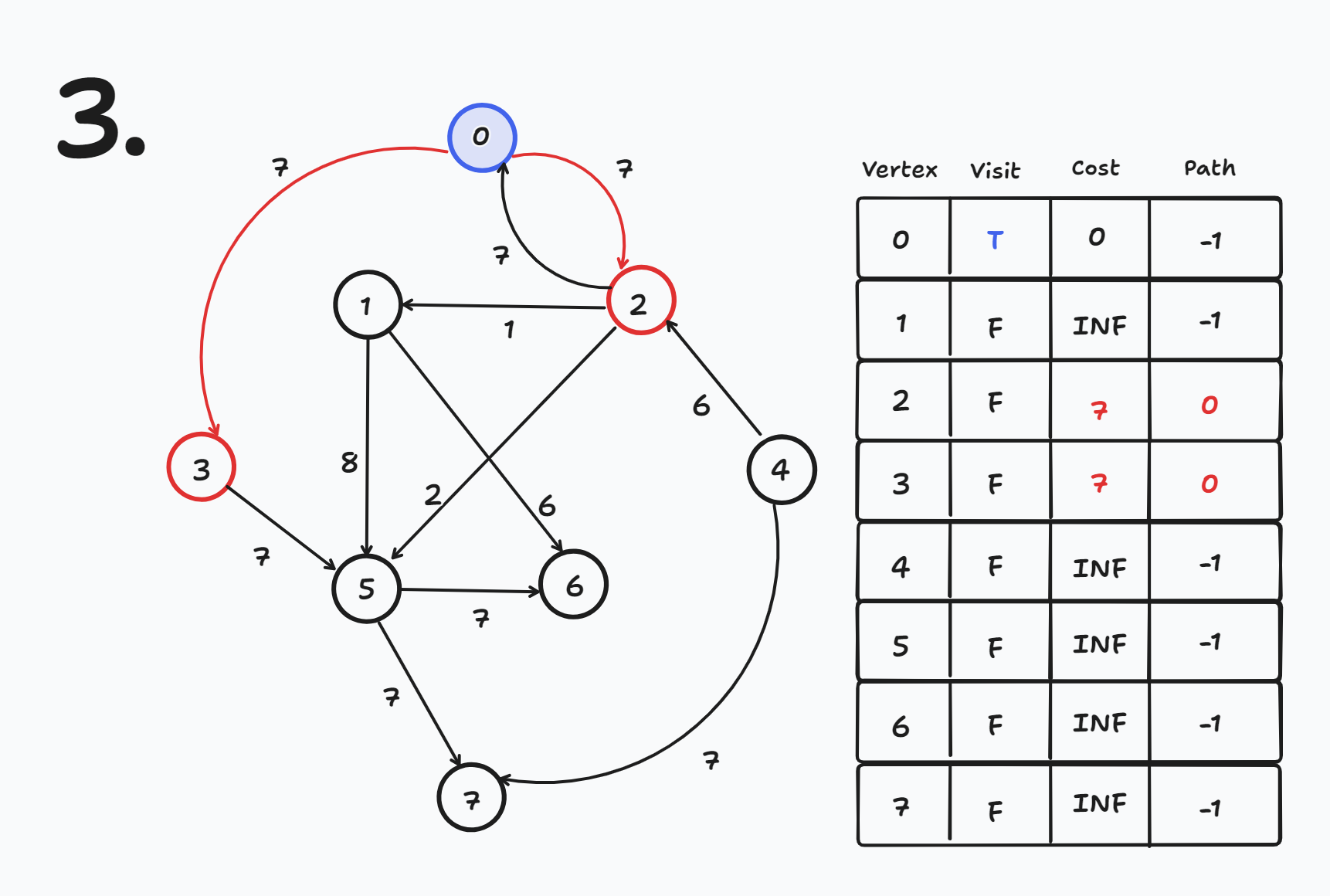
현재 노드에서 나가는 간선들에 대해 목적지 노드의 cost와 path를 갱신한다.
- 현재 노드가 0번 노드이므로 0번 노드에서 나가는 간선들에 대해 목적지 노드의 cost와 path를 갱신한다.
- cost[2] = 7, path[2] = 0
- cost[3] = 7, path[3] = 0
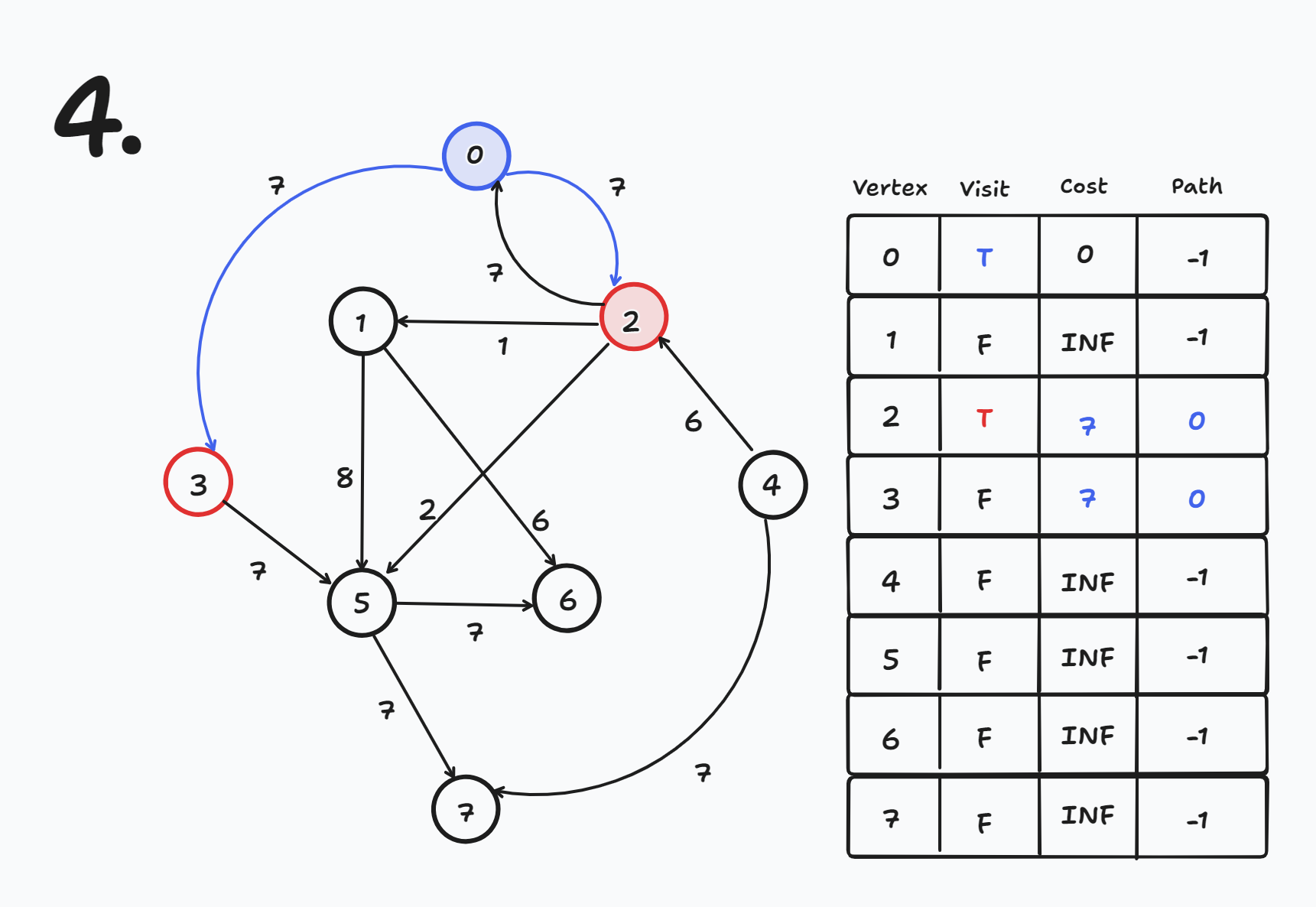
방문하지 않은 노드들 중 cost가 가장 작은 노드를 방문한다
- 현재 방문하지 않은 노드들 중 cost가 가장 작은 노드는 2,3번인데 index순서에 따라 2번 노드를 방문한다
- visit[2] = true
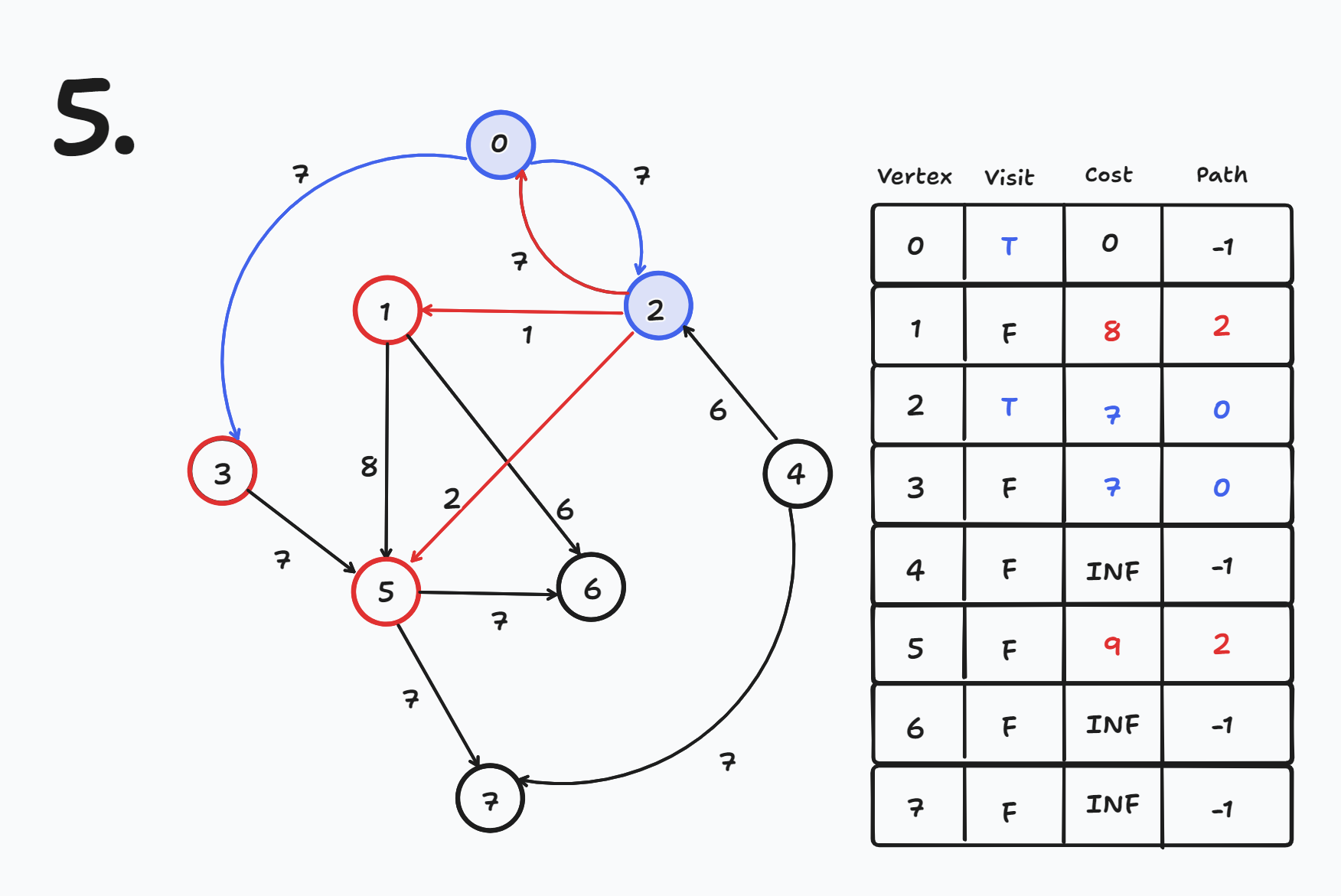
현재 노드에서 나가는 간선들에 대해 목적지 노드의 cost와 path를 갱신한다.
- 현재 노드가 2번이므로 2번 노드에서 나가는 간선에 대해 목적지 노드의 cost와 path를 갱신한다.
- cost[0] = 0 (0 < cost[2] + 7), path[0] = -1 (갱신 X)
- cost[1] = 8 (INF > cost[2] + 1), path[1] = 2 (갱신 O)
- cost[5] = 9 (INF > cost[2] + 2), path[5] = 2 (갱신 O)
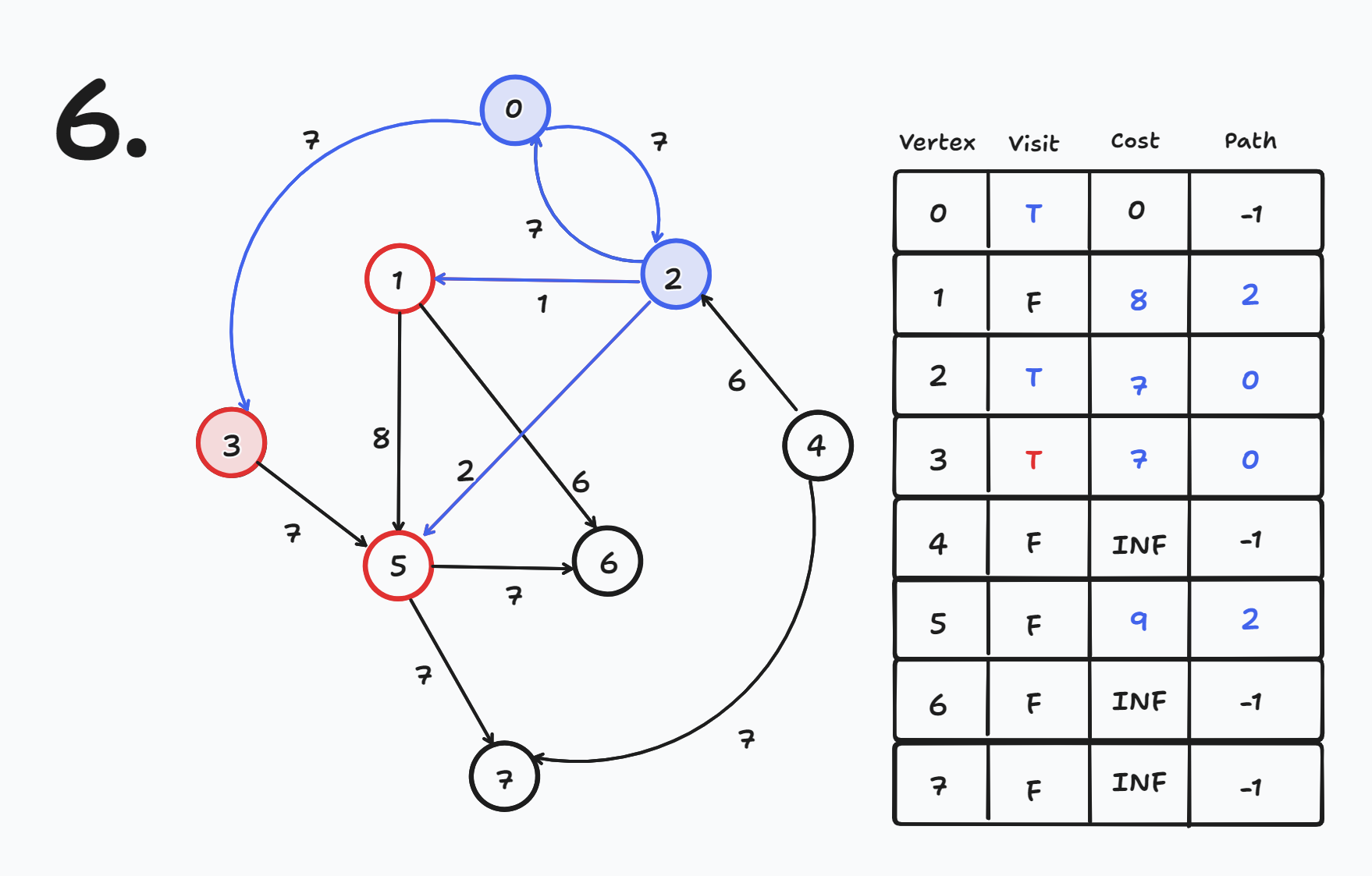
방문하지 않은 노드들 중 cost가 가장 작은 노드를 방문한다.
- 현재 방문하지 않은 노드들 중 cost가 가장 작은 노드는 3번이므로 3번 노드를 방문한다.
- visit[3] = true
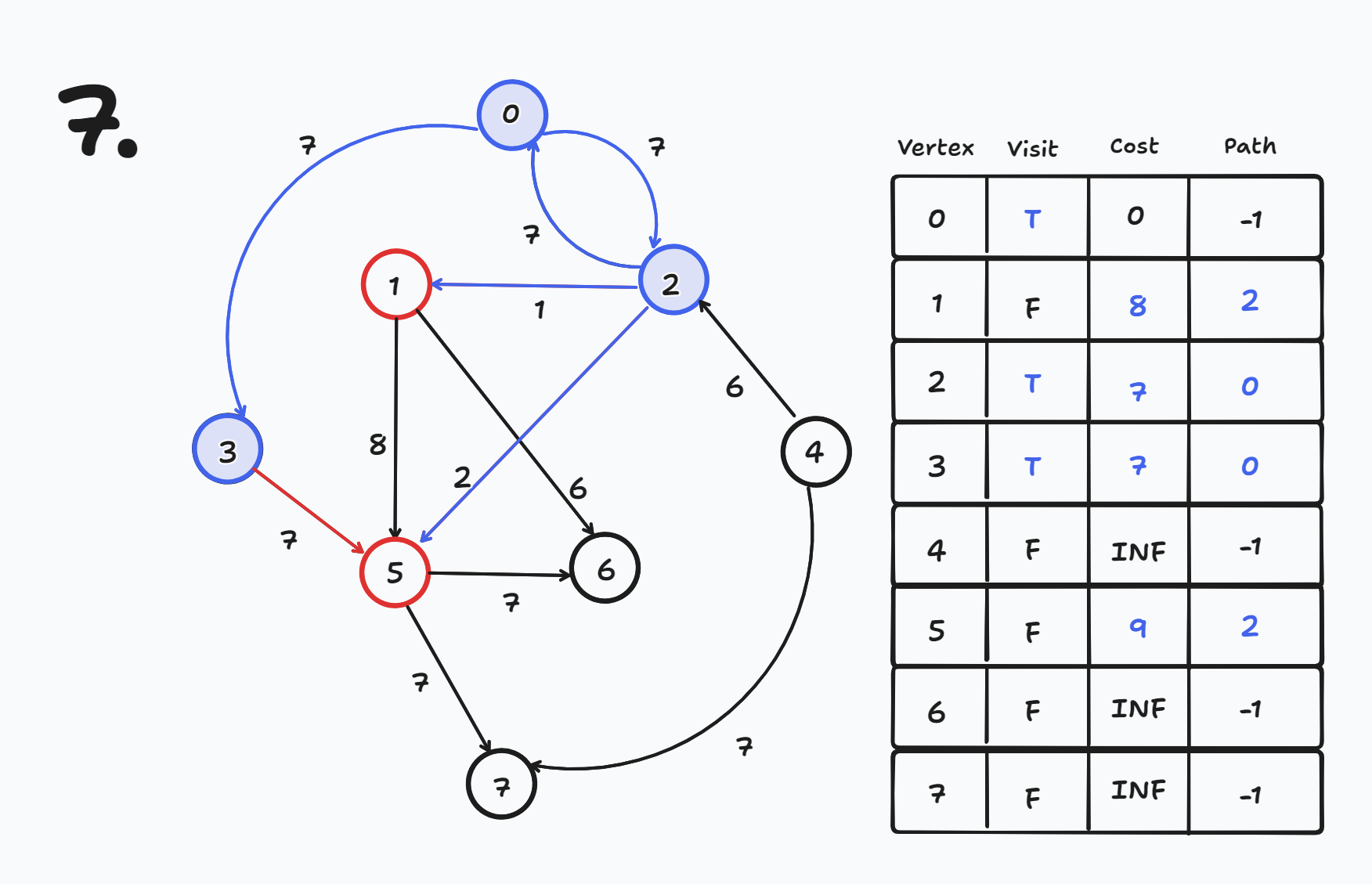
현재 노드에서 나가는 간선들에 대해 목적지 노드의 cost와 path를 갱신한다.
- 현재 노드가 3번이므로 3번 노드에서 나가는 간선에 대해 목적지 노드의 cost와 path를 갱신한다.
- cost[5] = 9 (9 < cost[3] + 7), path[5]=2 (갱신 X)
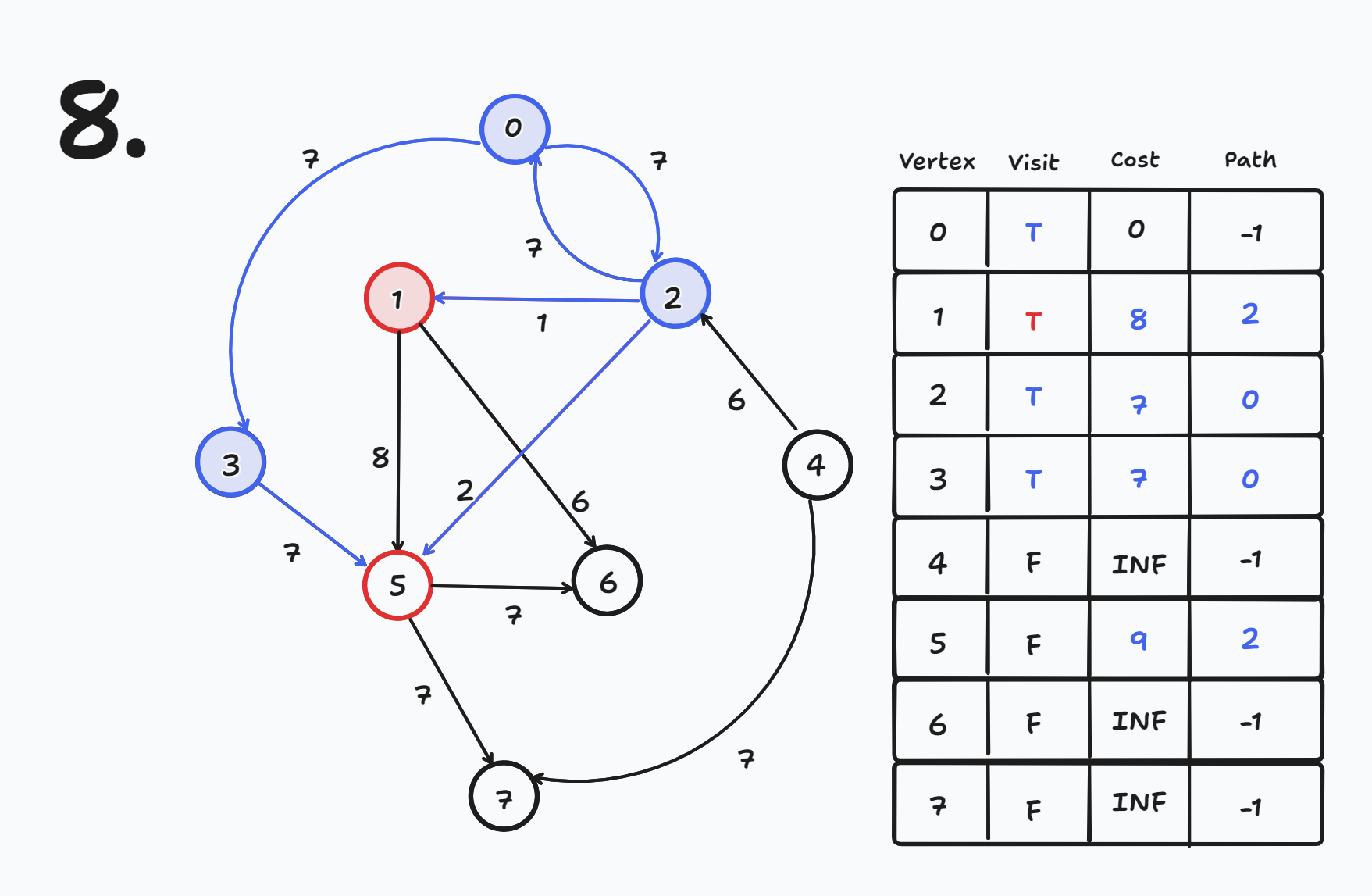
방문하지 않은 노드들 중 cost가 가장 작은 노드를 방문한다.
- 현재 방문하지 않은 노드들 중 cost가 가장 작은 노드는 1번이므로 1번 노드를 방문한다.
- visit[1] = true
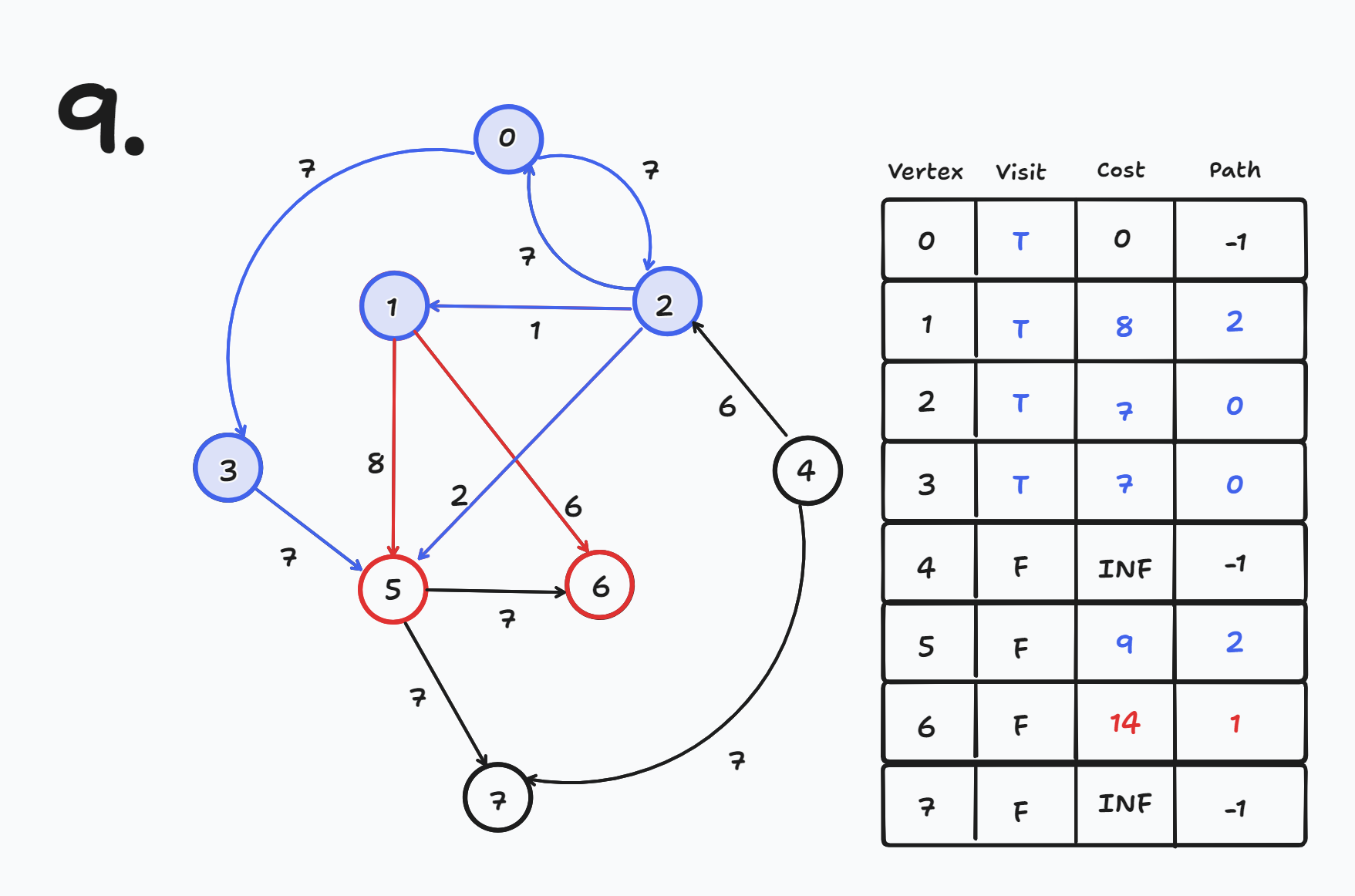
현재 노드에서 나가는 간선들에 대해 목적지 노드의 cost와 path를 갱신한다.
- 현재 노드가 1번이므로 1번 노드에서 나가는 간선에 대해 목적지 노드의 cost와 path를 갱신한다.
- cost[5] = 9 (9 < cost[1] + 8), path[5] = 2 (갱신 X)
- cost[6] = 14 (INF > cost[1] + 6), path[6] = 1 (갱신 O)
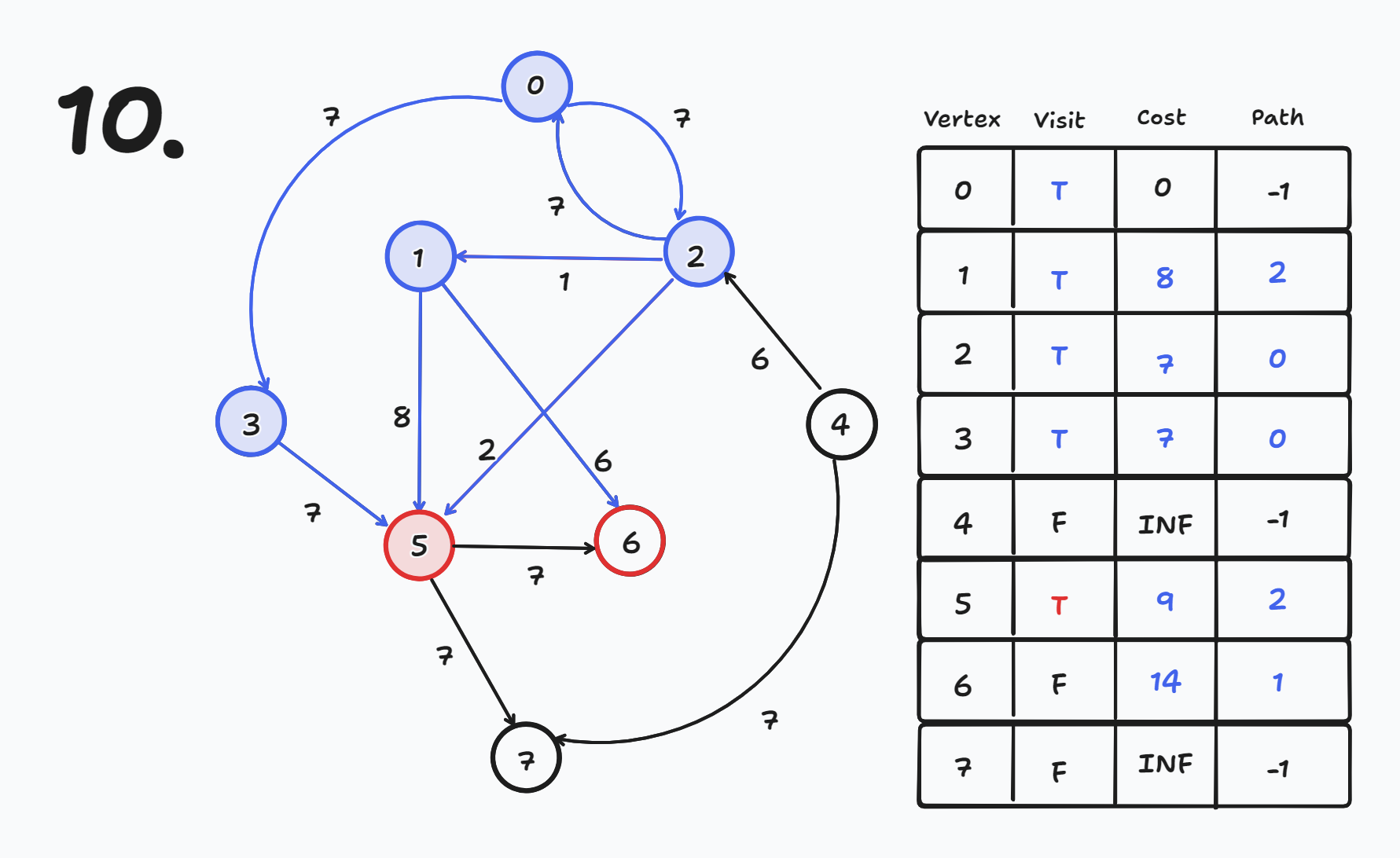
방문하지 않은 노드들 중 cost가 가장 작은 노드를 방문한다.
- 현재 방문하지 않은 노드들 중 cost가 가장 작은 노드는 5번이므로 5번 노드를 방문한다.
- visit[5] = true
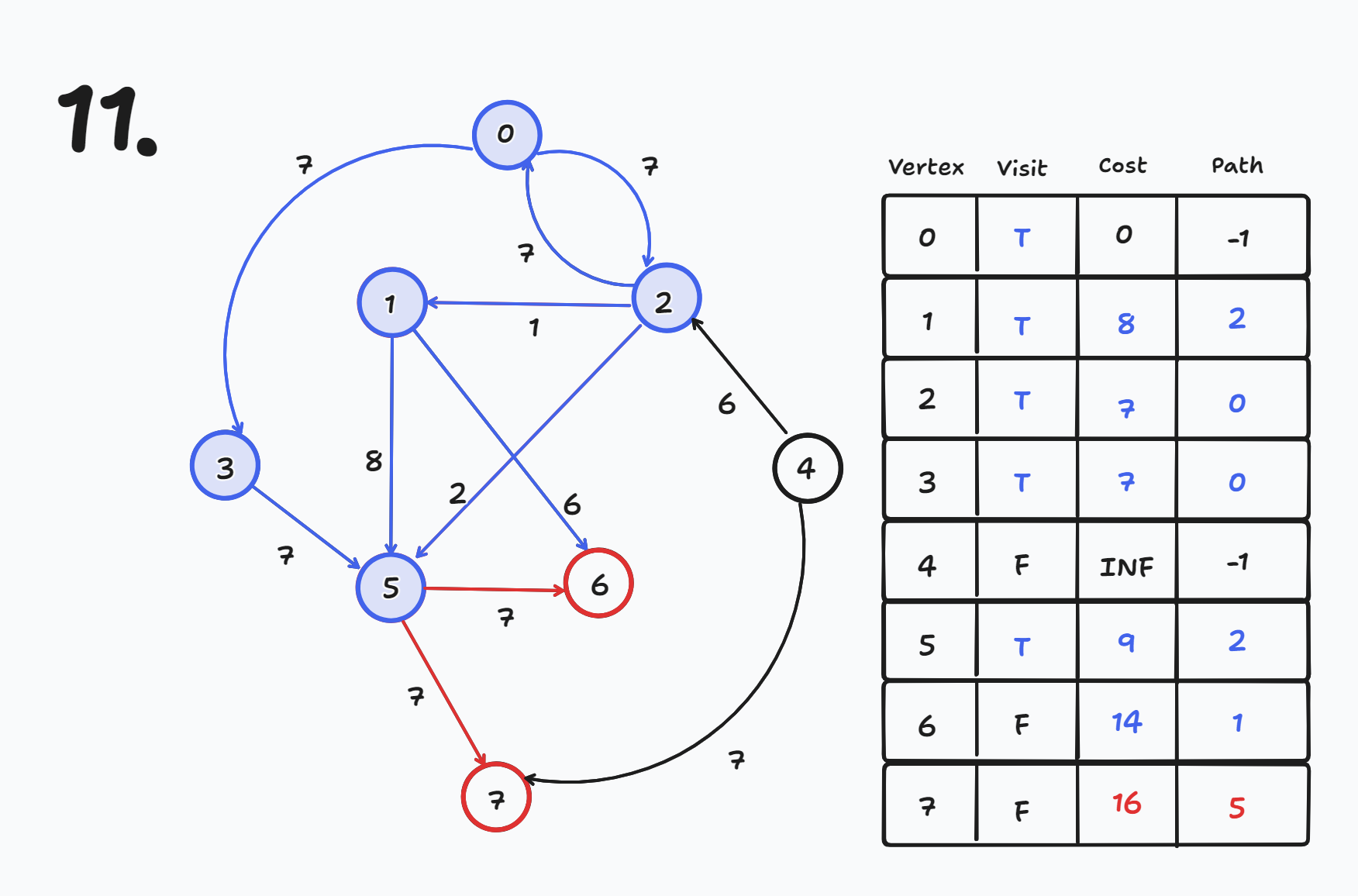
현재 노드에서 나가는 간선들에 대해 목적지 노드의 cost와 path를 갱신한다.
- 현재 노드가 5번이므로 5번 노드에서 나가는 간선에 대해 목적지 노드의 cost와 path를 갱신한다.
- cost[6] = 14 (14 < cost[5] + 7), path[6] = 1 (갱신 X)
- cost[7] = 16 (INF < cost[5] + 7), path[7] = 5 (갱신 O)
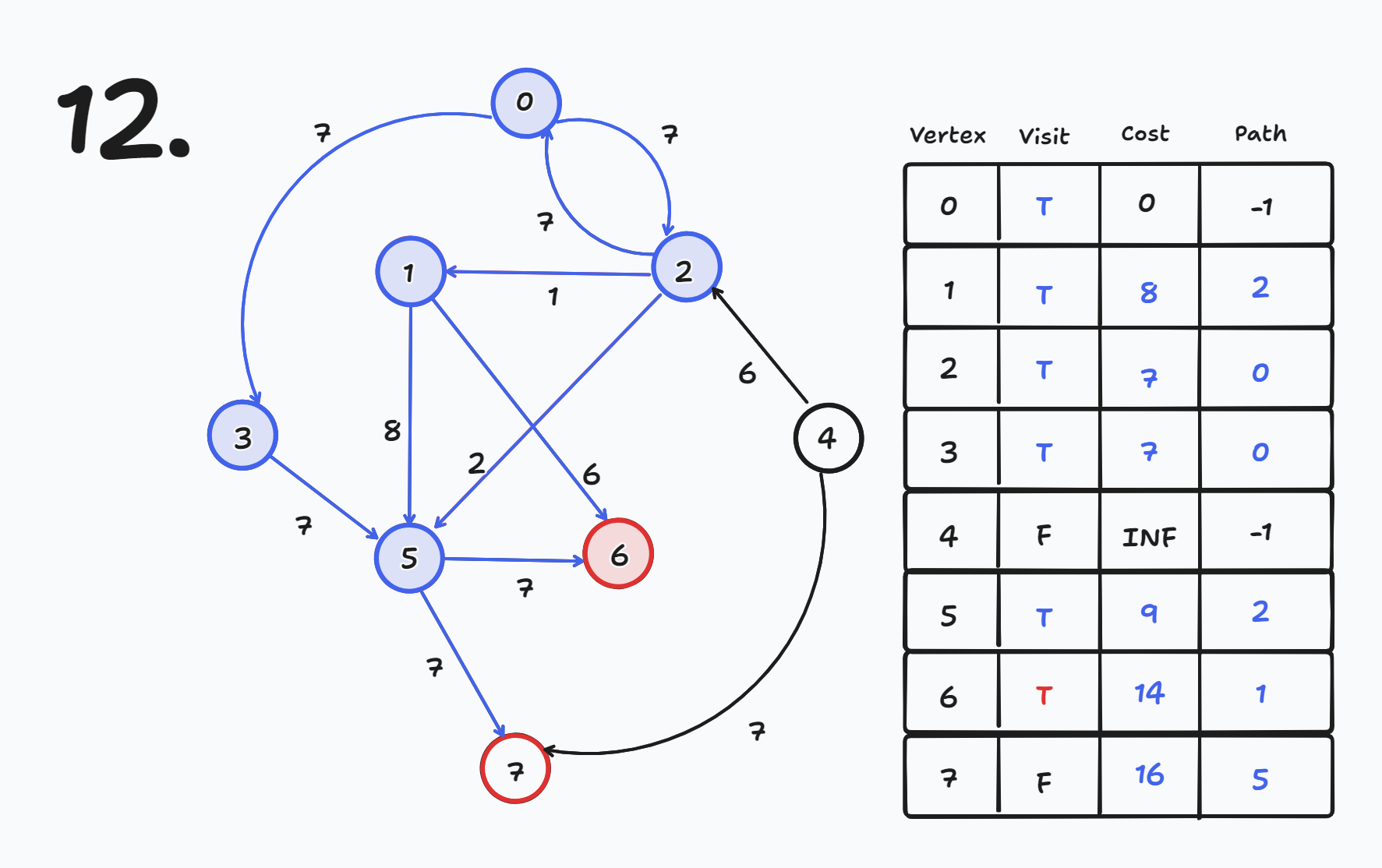
방문하지 않은 노드들 중 cost가 가장 작은 노드를 방문한다.
- 현재 방문하지 않은 노드들 중 cost가 가장 작은 노드는 6번이므로 6번 노드를 방문한다.
- visit[6] = true
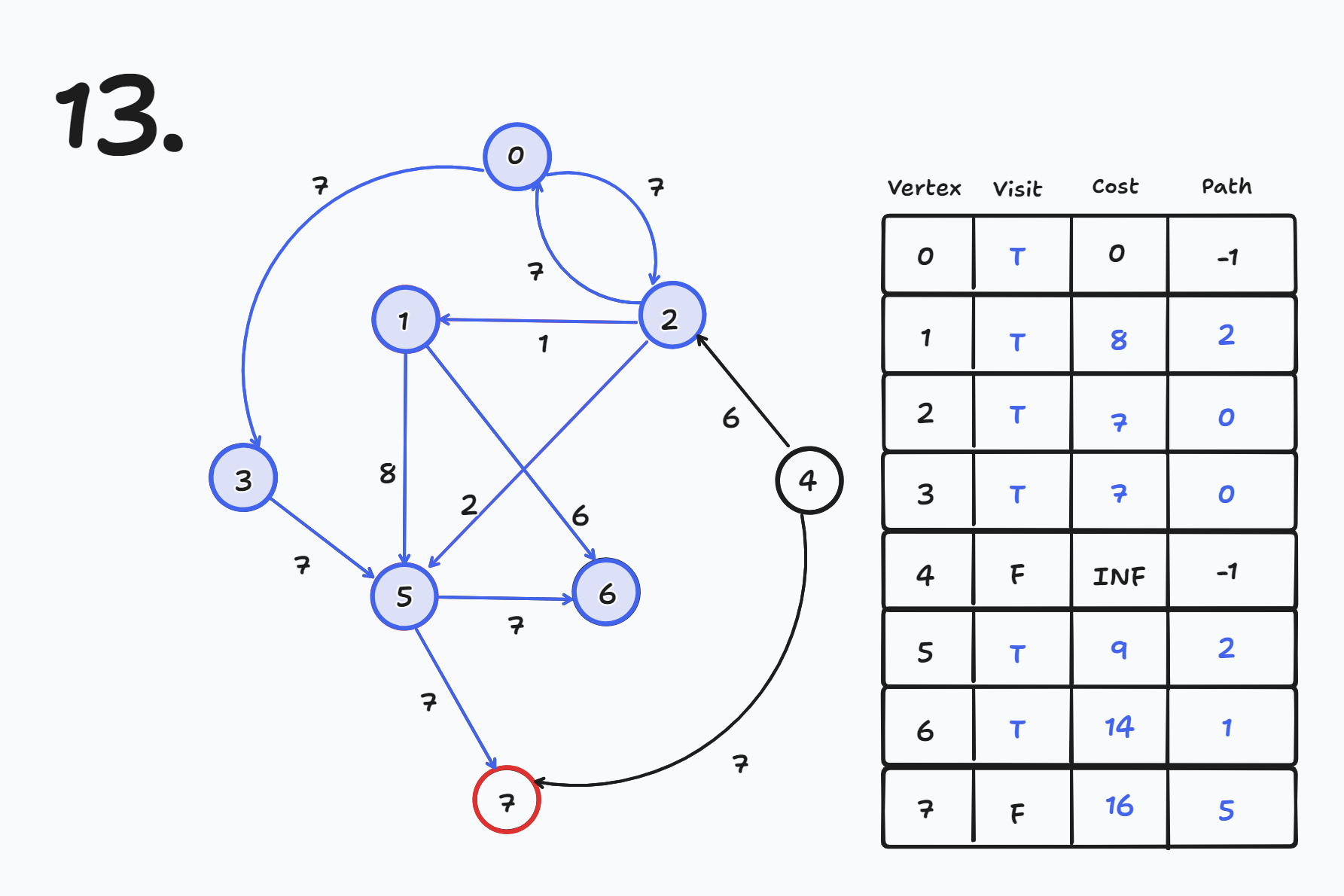
현재 노드에서 나가는 간선들에 대해 목적지 노드의 cost와 path를 갱신한다.
- 현재 노드가 6번이므로 6번 노드에서 나가는 간선에 대해 목적지 노드의 cost와 path를 갱신한다.
- 6번 노드에서 나가는 간선이 없기 때문에 그냥 종료
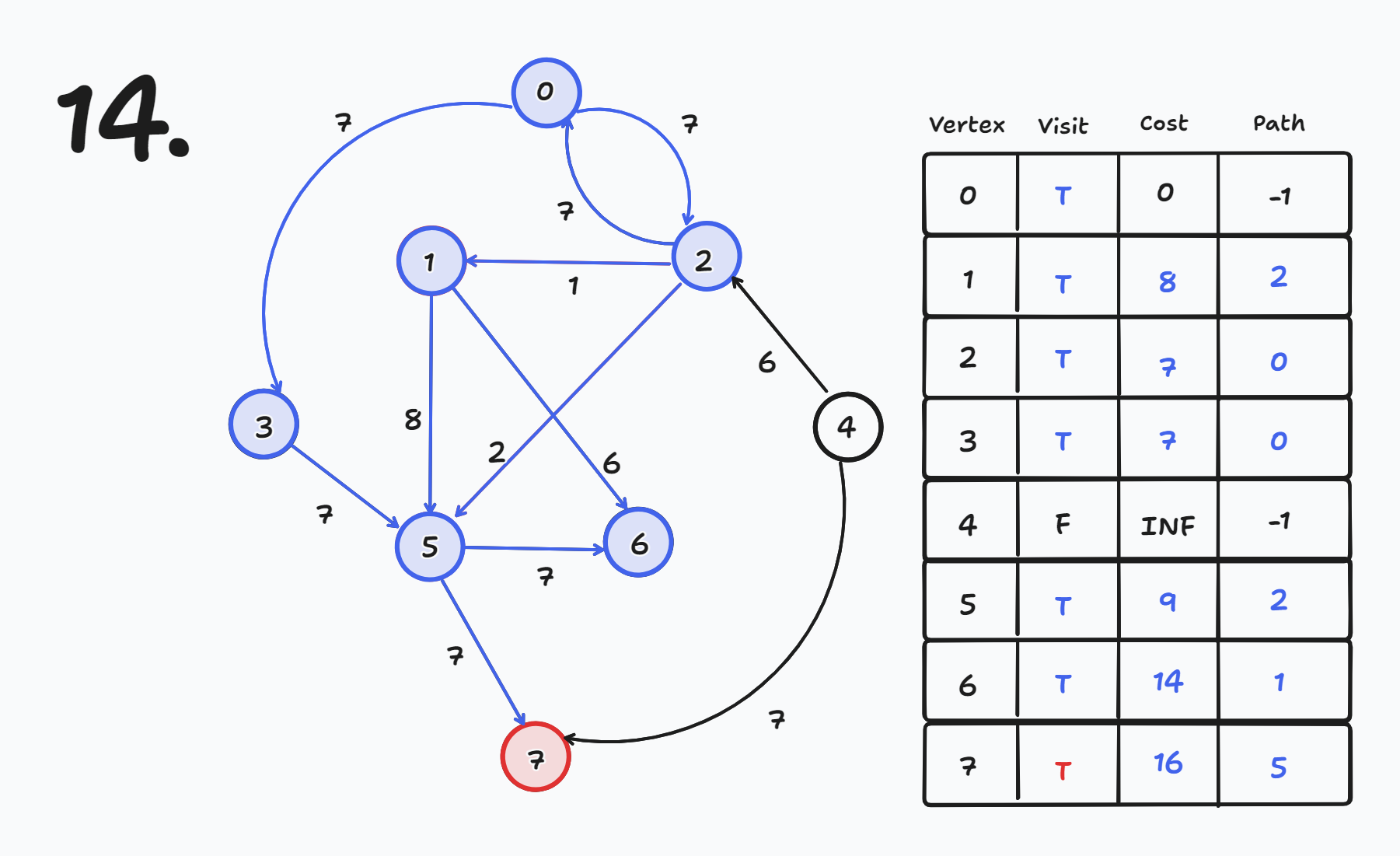
방문하지 않은 노드들 중 cost가 가장 작은 노드를 방문한다.
- 현재 방문하지 않은 노드들 중 cost가 가장 작은 노드는 7번이므로 7번 노드를 방문한다.
- visit[7] = true
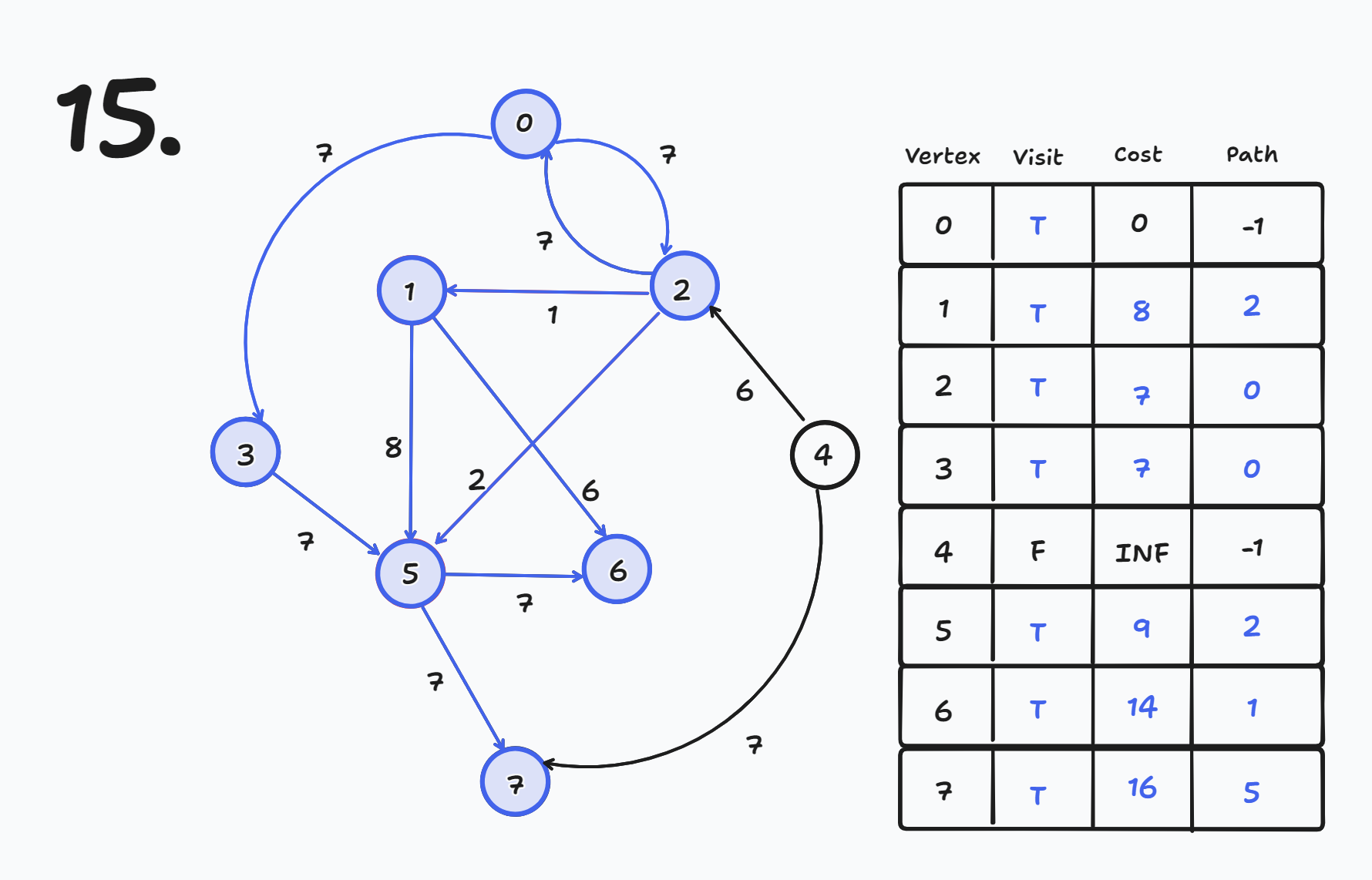
현재 노드에서 나가는 간선들에 대해 목적지 노드의 cost와 path를 갱신한다.
- 현재 노드가 7번이므로 7번 노드에서 나가는 간선에 대해 목적지 노드의 cost와 path를 갱신한다.
- 7번 노드에서 나가는 간선이 없기 때문에 그냥 종료
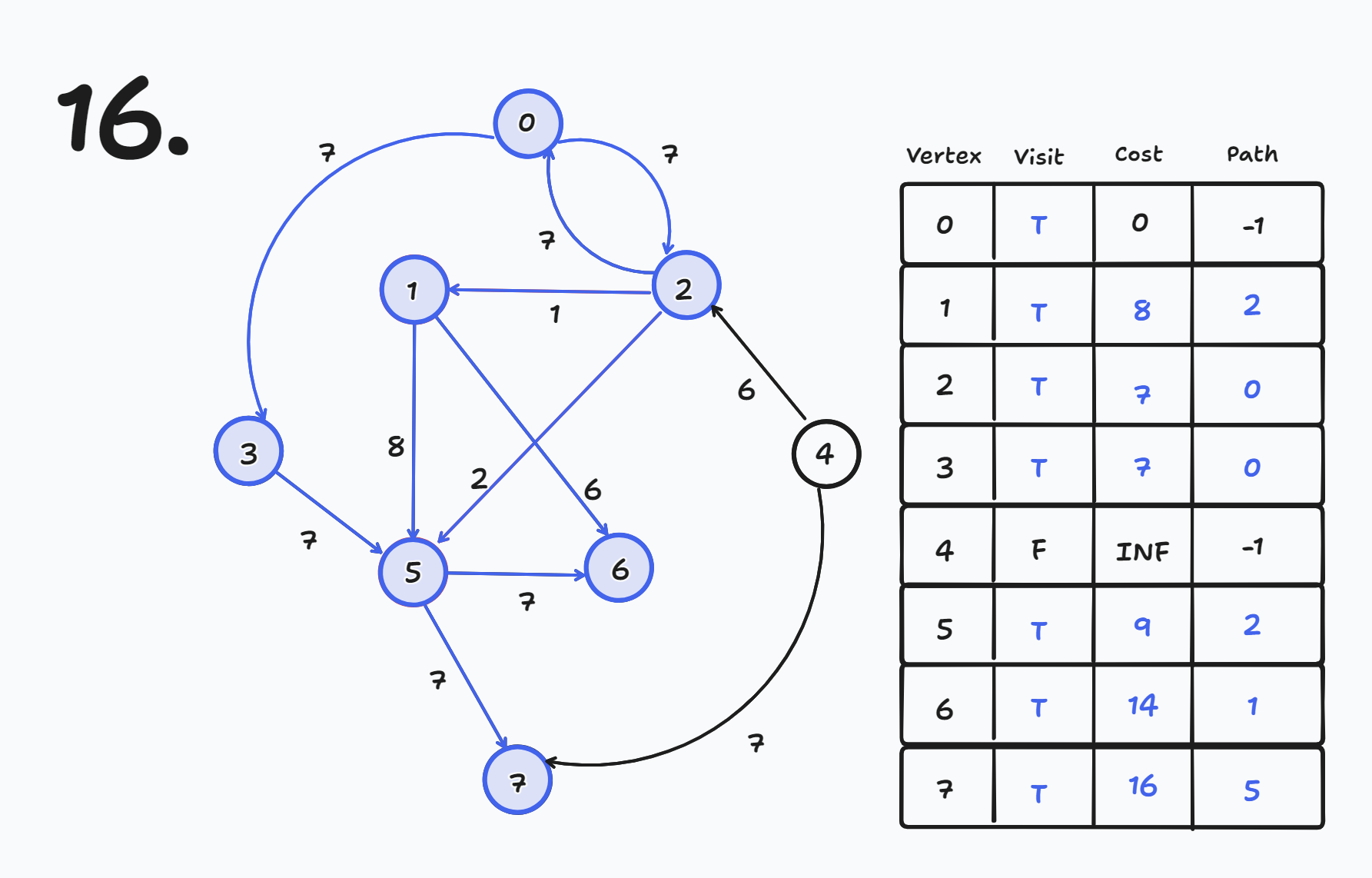
방문하지 않은 노드들 중 cost가 가장 작은 노드를 방문한다.
- 현재 방문하지 않은 노드는 4번 뿐인데, 출발 노드인 0번 노드에서 4번 노드로 가는 경로가 없기 때문에 그냥 종료한다.
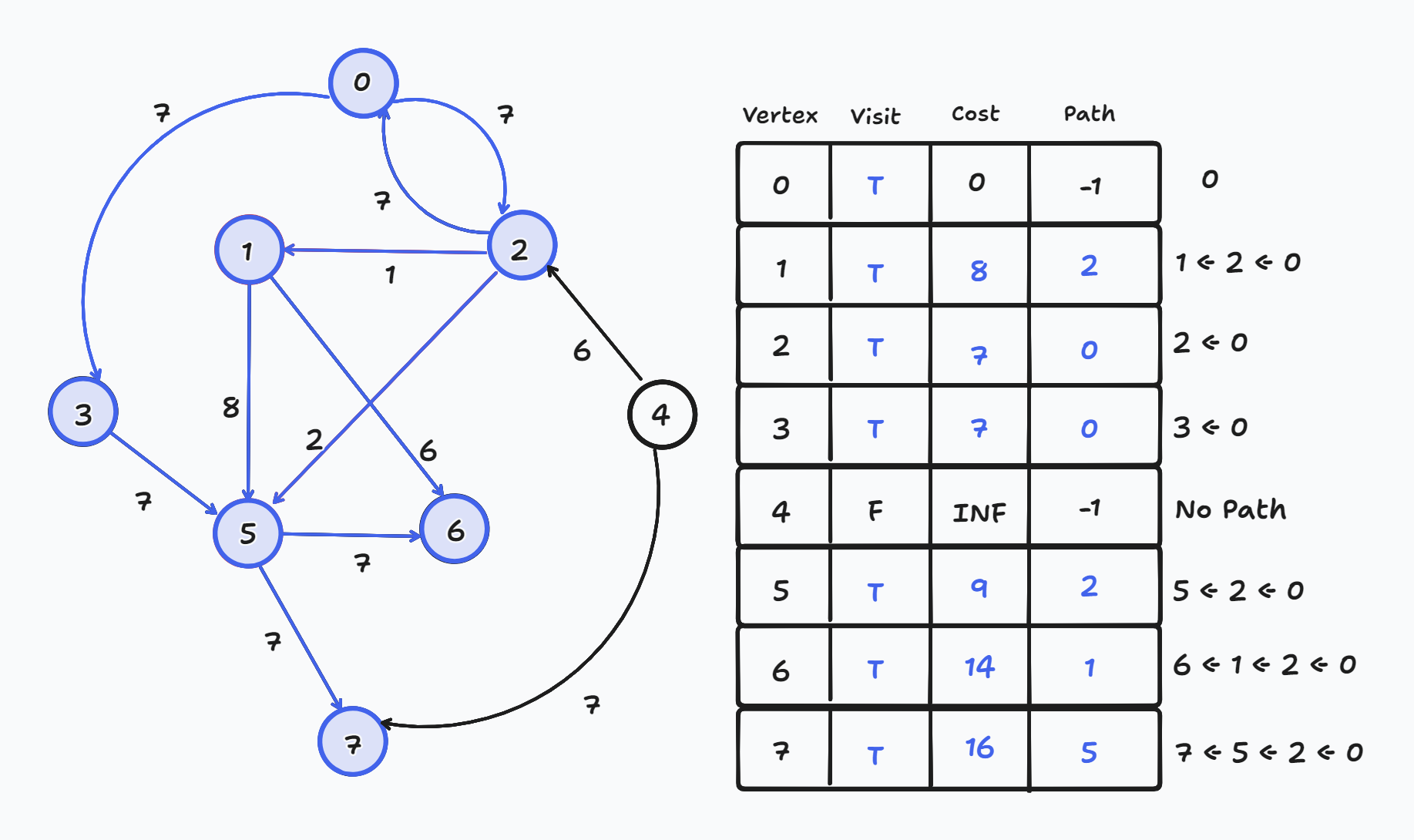
종료, 출발 노드인 0번 노드로부터 각 노드의 최단 경로와 그 길이이다.
# 코드 (Java)
의사 코드
// 우선순위 큐 없이
Dijkstra(G, w, S) {
Init(G, S)
visit = {}
cost[S] = 0
for ( i = 0; i<N; i++) {
u = find_minimum_node_not_visit()
visit[u] = true
for each v of adjacent u {
if cost[v] > cost[u] + w(u,v)
then cost[v] = cost[u] + w(u,v)
and path[v] = u
}
}
}
// 우선순위 큐 사용
Dijkstra(G, w, S) {
Init(G, S)
visit = {}
cost[S] = 0
pq.add(S, cost[S])
while(pq is not empty) {
u = extract_min(pq)
visit[u] = true
for each v of adjacent u {
if cost[v] > cost[u] + w(u,v)
then cost[v] = cost[u] + w(u,v)
and path[v] = u
}
}
}시간복잡도
우선순위 큐 없을 시: O(n^2)
우선순위 큐 사용 시: (mlogn^2)
n: 노드 개수, m: 간선 개수
코드 (Java, 우선순위 큐 사용)
public class Dijkstra {
static int[] minDistanceFromSource;
static int[] predecessor;
static int vertexCount;
static int edgeCount;
static int source;
static List<Edge>[] graph;
public static void main(String[] args) throws IOException {
// initGraph() -> 이 부분은 상황에 따라 달라지므로 단순히 이렇게 표현
dijkstra();
}
private static int[] dijkstra() {
PriorityQueue<Edge> queue = new PriorityQueue<>(Comparator.comparing(x -> x.weight));
minDistanceFromSource = new int[vertexCount + 1];
predecessor = new int[vertexCount + 1];
boolean[] visit = new boolean[vertexCount + 1];
for (int i = 1; i <= vertexCount; i++) {
distance[i] = Integer.MAX_VALUE;
}
distance[source] = 0;
queue.add(new Edge(source, source, 0));
while (!queue.isEmpty()) {
Edge minEdge = queue.remove();
visit[Edge.to] = true;
for (Edge adjEdge : graph[minEdge.to]) {
if (distance[adjEdge.to] > distance[adjEdge.from] + adjEdge.weight) {
distance[adjEdge.to] = distance[adjEdge.from] + adjEdge.weight;
queue.add(new Edge(adjEdge.from, adjEdge.to, distance[adjEdge.to]));
predecessor[adjEdge.to] = adjEdge.from;
}
}
}
return distance;
}
}
class Edge {
int from;
int to;
int weight
public Edge(int from, int to, int weight) {
this.from = from;
this.to = to;
this.weight = weight;
}
}
# Reference
권오흠 교수님 유튜브 및 강의자료
알고리즘 Visualization
Data Structure Visualization
www.cs.usfca.edu
'Algorithm' 카테고리의 다른 글
| [Algorithm] Bellman-Ford(벨만포드) 알고리즘 (1) | 2024.01.25 |
|---|---|
| [Algorithm] 최단 경로 문제 (Shortest Path Problem) (1) | 2024.01.24 |
| [Algorithm] Prim(프림) 알고리즘 (0) | 2022.01.16 |
| [Algorithm] Krsukal (크루스칼) 알고리즘 (0) | 2022.01.16 |
| [Algorithm] MST (Minimum Spanning Tree, 최소 신장 트리) (0) | 2022.01.16 |