1. 문제
programmers.co.kr/learn/courses/30/lessons/43105
코딩테스트 연습 - 정수 삼각형
[[7], [3, 8], [8, 1, 0], [2, 7, 4, 4], [4, 5, 2, 6, 5]] 30
programmers.co.kr
문제 설명

제한 사항

입출력 예

2. 어떻게 풀까?
- 문제에서 그림은 실제로 보면 직삼각형이다.
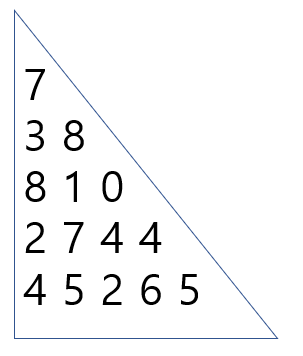
- 7부터 아래로 내려가면서 값을 더한다, 겹치는 칸은 더 큰 값을 할당한다.


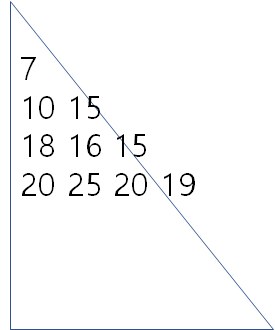
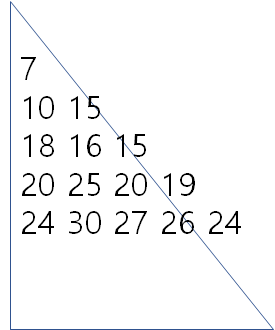
- 배열의 처음과 끝은, 대소 비교를 할 필요 없이 현재 값과 이전 행의 같은 열 값을 더한 값이다
- 그 외에는 이전 행의 같은 열과 이전 행중에서 큰 값과 더한 값이다.
3. 코드
테스트 코드
import static org.hamcrest.CoreMatchers.is;
import static org.junit.Assert.*;
import org.junit.Test;
public class SolutionTest {
@Test
public void test1() {
int[][] triangle = {
{7},
{3, 8},
{8, 1, 0},
{2, 7, 4, 4},
{4, 5, 2, 6, 5}
};
assertThat(new Solution().solution(triangle), is(30));
}
}실제 코드
import java.util.Arrays;
public class Solution {
public int solution(int[][] triangle) {
int[][] maxSums = init(triangle);
for (int row = 1; row < triangle.length; row++) {
fillFirstAndLast(maxSums, triangle, row);
for (int j = 1; j < maxSums[row].length - 1; j++) {
maxSums[row][j] = Math.max(maxSums[row - 1][j - 1], maxSums[row - 1][j])
+ triangle[row][j];
}
}
return Arrays.stream(maxSums[maxSums.length - 1]).max().getAsInt();
}
private void fillFirstAndLast(int[][] maxSums, int[][] triangle, int row) {
int first = 0;
int last = maxSums[row].length - 1;
maxSums[row][first] = maxSums[row - 1][first] + triangle[row][first];
maxSums[row][last] = maxSums[row - 1][last - 1] + triangle[row][last];
}
private int[][] init(int[][] triangle) {
int[][] result = new int[triangle.length][];
for (int i = 0; i < triangle.length; i++) {
result[i] = new int[triangle[i].length];
}
result[0][0] = triangle[0][0];
return result;
}
}
init()에서 배열을 생성하고 (0,0)에triangle[0][0]을 할당한다.fillFirstAndLast()에서 현재 행의 처음 열과 마지막 열의 값을 할당한다.- 그리고 그 외의 값은 이전 행의 같은 열과, 이전 열중 더 큰 값과 현재 값을 더한 값을 할당한다.
Best 코드 (내가 보기에 Best)
import java.util.Arrays;
public class BestAnswer {
public static int solution(int[][] triangle) {
for (int row = 1; row < triangle.length; row++) {
triangle[row][0] += triangle[row - 1][0];
triangle[row][row] += triangle[row - 1][row - 1];
for (int col = 1; col < row; col++) {
triangle[row][col] += Math.max(triangle[row - 1][col], triangle[row - 1][col - 1]);
}
}
return Arrays.stream(triangle[triangle.length - 1]).max().getAsInt();
}
}
- 굳이 새 배열을 생성하지 않고, 현재 값에 최대값을 더한 값을 할당해준다.
triangle[row][triangle[row].length-1]보다triangle[row][row]가 훨씬 깔끔해 보인다.
4. 느낀 점
- 예전에 비슷한 문제를 풀어본 기억이 나서 쉽게 풀었다.
'Coding Test > Programmers' 카테고리의 다른 글
| [Programmers] 단어 변환 (Java) (0) | 2022.01.26 |
|---|---|
| 프로그래머스 - 자물쇠와 열쇠 (java) (0) | 2021.02.25 |
| 프로그래머스 - N으로 표현(02/02) (java) (0) | 2021.02.02 |
| 프로그래머스 - 추석 트래픽(01/23) (java) (0) | 2021.01.23 |
| 프로그래머스 - 압축 (01/11) (java) (0) | 2021.01.11 |





