그래프 순회
- 그래프에서 임의의 한 정점에서 출발하여 모든 정점을 한번씩 방문하는 작업
- 탐색하는 동안 이미 방문한 정점이 있을 수 있으므로 방문했다는 표시를하여 중복방문을 피한다.
- 대표적으로 DFS와 BFS가 있다.
DFS (Depth-First-Search): 깊이 우선 탐색
- 출발노드에서 하위노드(자식노드)를 먼저 탐색하는 방식
- 일반적으로 Stack이나 Recursive를 이용하여 구현한다.
동작방식
- 시작노드에서 간선을 따라 다음노드로 방문한다.
- 더이상 탐색할 간선이 없다면 역추적(Backtracking)을 통해 이전노드로 이동하여 아직 탐색하지 않은 간선을 참색한다.
- 모든 노드를 탐색할 때까지 반복한다.
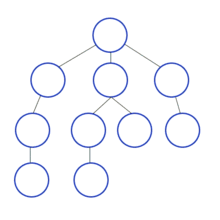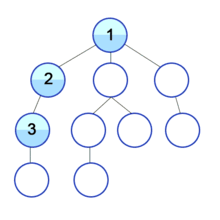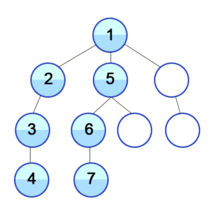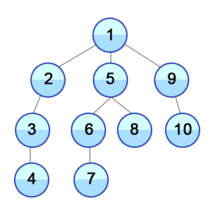
Visualize

E노드에서 더이상 이동 할 간선이 없으므로 역추적으로 통해 B노드로 이동, B노드에서도 마찬가지로 더이상 이동할 간선이 없으므로 A노드로 이동 후 다음 간선인 (A,C)을 통해 C노드로 이동

F노드에서 더이상 이동할 간선이 없으므로 역추적을 통해 C노드로 이동, C노드에서 다음 간선인 (C,G)을 통해 G노드로 이동

I노드에서 더이상 이동할 간선이 없으므로 역추적을 통해 G노드로 이동, G노드에서도 마찬가지로 C노드로 이동, C노드에서도 마찬가지로 A노드로 이동, A노드에서 다음 간선인 (A,D)를 통해 D노드로 이동

코드
의사코드
DFS(graph, current_node, visit) {
visit[current_node] = true
for( adjacent_node to current_node) {
if(!visit[adjacent_node]) {
DFS(graph, adjacent_node, visit)
}
}
}코드 - Recursive (Java)
class DFS_Recursive {
private int[][] graph;
private boolean[] visit;
public DFS_Recursive() {
this.graph = {
{0, 1, 1, 1, 0, 0, 0, 0, 0},
{1, 0, 0, 0, 1, 0, 0, 0, 0},
{1, 0, 0, 0, 0, 1, 1, 0, 0},
{1, 0, 0, 0, 0, 0, 0, 1, 0},
{0, 1, 0, 0, 0, 0, 0, 0, 0},
{0, 0, 1, 0, 0, 0, 0, 0, 1},
{0, 0, 1, 0, 0, 0, 0, 0, 0},
{0, 0, 0, 1, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 1, 0, 0, 0},
};
visit = new boolean[graph.length];
}
public void dfs(currentNode) {
visit[currentNode] = true;
for(int i = 0; i < graph[currentNode].length; i++) {
if(isAdjacentNode(currentNode, i) && !visit[i]) {
dfs(i);
}
}
}
public boolean isAdjacentNode(int currentNode, int targetNode) {
return graph[currentNode][targetNode] == 1;
}
}코드 - Stack
class DFS_Stack {
private int[][] graph;
private boolean[] visit;
public DFS_Stack() {
this.graph = {
{0, 1, 1, 1, 0, 0, 0, 0, 0},
{1, 0, 0, 0, 1, 0, 0, 0, 0},
{1, 0, 0, 0, 0, 1, 1, 0, 0},
{1, 0, 0, 0, 0, 0, 0, 1, 0},
{0, 1, 0, 0, 0, 0, 0, 0, 0},
{0, 0, 1, 0, 0, 0, 0, 0, 1},
{0, 0, 1, 0, 0, 0, 0, 0, 0},
{0, 0, 0, 1, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 1, 0, 0, 0},
};
visit = new boolean[graph.length];
}
public void dfs(startNode) {
Stack<Integer> stack = new Stack();
stack.push(startNode);
visit[startNode] = true;
while(!stack.isEmpty()) {
int currentNode = stack.pop();
for(int i = 0; i < graph[currentNode].length; i++) {
if(isAdjacentNode(i) && !visit[i]) {
stack.push(i);
visit[i] = true;
}
}
}
}
public boolean isAdjacentNode(int currentNode, int targetNode) {
return graph[currentNode][targetNode] == 1;
}
}시간복잡도
- 인접 리스트: \(O(N+E)\) (\(N\): 정점 개수, \(E\): 간선 개수)
- 인접 행렬: \(O(N^2)\)
참고
2021.04.14 - [Algorithm] - [Algorithm] 그래프 (Graph)
[Algorithm] 그래프 (Graph)
참고1 : 유튜브 (권오흠 교수, 2015 봄학기 알고리즘) 참고2 : (다양한 예제로 학습하는) 데이터 구조와 알고리즘 for java 1. 그래프 : G = (V, E) 1. 정의 V : 정점(Vertex) 또는 노드(Node)들의 집합 E : 간선,..
jino-dev-diary.tistory.com
2022.01.08 - [Algorithm] - [Algorithm] BFS (Breath-First-Search, 너비 우선 탐색)
[Algorithm] BFS (Breath-First-Search, 너비 우선 탐색)
그래프 순회 그래프에서 임의의 한 정점에서 출발하여 모든 정점을 한번씩 방문하는 작업 탐색하는 동안 이미 방문한 정점이 있을 수 있으므로 방문했다는 표시를 하여 중복방문을 피한다. 대
jino-dev-diary.tistory.com
'Algorithm' 카테고리의 다른 글
| [Algorithm] MST (Minimum Spanning Tree, 최소 신장 트리) (0) | 2022.01.16 |
|---|---|
| [Algorithm] BFS (Breath-First-Search, 너비 우선 탐색) (0) | 2022.01.08 |
| [Algorithm] 정렬 - Heap Sort (힙 정렬) (0) | 2021.09.29 |
| [Algorithm] 정렬 - Quick Sort (퀵 정렬) (1) | 2021.09.18 |
| [Algorithm] 정렬 - Merge Sort (합병 정렬) (0) | 2021.09.17 |